
分析 (Ⅰ)利用直接法,求动点P的轨迹C的方程;
(Ⅱ)求出M,N的坐标,可得以MN为直径的圆的方程,即可得出结论.
解答  解:(Ⅰ)设点P的坐标为(x,y),因为动点P到定直线l:x=-2的距离比到定点F($\frac{1}{2}$,0)的距离大$\frac{3}{2}$,
解:(Ⅰ)设点P的坐标为(x,y),因为动点P到定直线l:x=-2的距离比到定点F($\frac{1}{2}$,0)的距离大$\frac{3}{2}$,
所以x>-2且$\sqrt{(x-\frac{1}{2})^{2}+{y}^{2}}$=|x+2|-$\frac{3}{2}$,
化简得y2=2x,
∴轨迹C的方程为y2=2x.
(Ⅱ)设A(2t12,2t1),B(2t22,2t2)(t1t2≠0),则
∵A,D,B三点共线,
∴2t2(2t12-2=2t1(2t22-2)),
又t1≠t2,∴t1t2=-1,
直线OA的方程为y=$\frac{1}{{t}_{1}}$x,令x=-2,得M(-2,-$\frac{2}{{t}_{1}}$).
同理可得N(-2,-$\frac{2}{{t}_{2}}$).
所以以MN为直径的圆的方程为(x+2)(x+2)+(y+$\frac{2}{{t}_{1}}$)(y+$\frac{2}{{t}_{2}}$)=0,
将t1t2=-1代入上式,可得(x+2)2+y2-2(t1+t2)y-4=0,
令y=0,即x=0或x=-4,
故以MN为直径的圆被x轴截得的弦长为定值4.
点评 本题考查轨迹方程,考查圆的方程,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | bn=2n | B. | bn=3n | C. | bn=2n-1 | D. | bn=3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∉(0,1),${x_0}^2-{x_0}≥0$ | B. | ?x0∈(0,1),${x_0}^2-{x_0}≥0$ | ||
| C. | ?x0∉(0,1),${x_0}^2-{x_0}<0$ | D. | ?x0∈(0,1),${x_0}^2-{x_0}≥0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
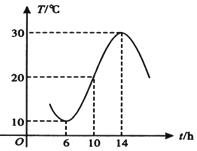 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b(|ϕ|<π),则这段曲线的函数解析式可以为y=10sin($\frac{π}{8}x+\frac{3π}{4}$)+20;(6≤x≤14).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com