
定义在R上的函数f(x)满足f(-x)=-f(x),f(x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x+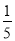 ,则f(log220)的值为( )
,则f(log220)的值为( )
A.1 B.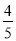 C.-1 D.-
C.-1 D.-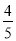
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:填空题
已知函数f(x)=sinx+ cosx(x∈R),函数y=f(x+φ)(|φ|≤
cosx(x∈R),函数y=f(x+φ)(|φ|≤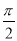 )的图象关于直线x=0对称,则φ的值为________.
)的图象关于直线x=0对称,则φ的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-7函数的图象(解析版) 题型:选择题
在函数y=|x|(x∈[-1,1])的图象上有一点P(t,|t|),此函数与x轴、直线x=-1及x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图象可表示为( )
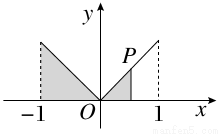
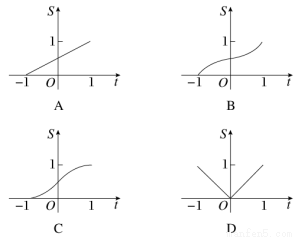
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-6对数与对数函数(解析版) 题型:解答题
是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,求出a的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-5指数及指数函数(解析版) 题型:解答题
定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,
f(x)=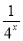 -
-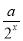 (a∈R).
(a∈R).
(1)求f(x)在[0,1]上的最大值;
(2)若f(x)是[0,1]上的增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-5指数及指数函数(解析版) 题型:选择题
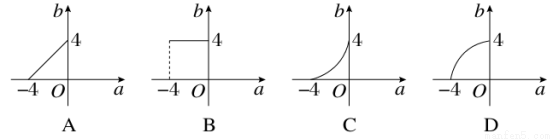
函数y=2|x|的定义域为[a,b],值域为[1,16],当a变化时,函数b=g(a)的图象可以是( )
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-4二次函数与幂函数(解析版) 题型:选择题
设函数f(x)=-2x2+4x在区间[m,n]上的值域是[-6,2],则m+n的取值所组成的集合为( )
A.[0,3] B.[0,4] C.[-1,3] D.[1,4]
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:解答题
甲同学家到乙同学家的途中有一公园,甲从家到公园的距离与乙从家到公园的距离都是2 km,甲10时出发前往乙家.如图所示,表示甲从家出发到达乙家为止经过的路程y(km)与时间x(分)的关系.试写出y=f(x)的函数解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com