
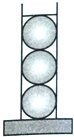
 圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
圆柱形容器内盛有高度为12cm的水,若放入三个不同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是科目:高中数学 来源: 题型:
| a |
| b |
| 16b |
| a |
| A、hmax(x) |
| B、(-∞,-2)∪(0,+∞) |
| C、(-4,2) |
| D、(-∞,-4)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
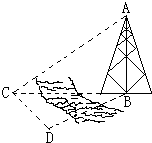 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
A、{x|x≠
| ||||
B、{x|x≠kπ+
| ||||
C、{x|x≠
| ||||
D、{x|x≠kπ-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com