Question

19．已知实数a，b满足0≤a≤2，0≤b≤1，则函数$y=\frac{1}{3}{x^3}-{x^2}+（a+b）x+c$有极值的概率（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{3}$
• C． $\frac{1}{2}$
• D． $\frac{2}{3}$

Answer 1

分析 利用函数的极值推出不等式，然后利用几何概型求解即可．

解答 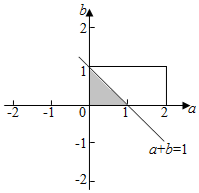解：函数$y=\frac{1}{3}{x^3}-{x^2}+（a+b）x+c$，
可得y′=x²-2x+a+b，函数$y=\frac{1}{3}{x^3}-{x^2}+（a+b）x+c$有极值，可知导函数有两个不相等的实数根．
可得4-4（a+b）＞0，即：a+b＜1．
如图：满足题意的阴影部分的面积为：$\frac{1}{2}$，符合条件的所有事件的面积为：2，
所求的概率为：$\frac{\frac{1}{2}}{2}$=$\frac{1}{4}$．
故选：A．

点评 本题考查函数的极值的条件的应用，几何概型的求法，考查数形结合转化思想的应用．