
分析 本题证明结论中结构较复杂,而其否定结构简单,故可用反证法证明其否定不成立,以此来证明结论成立.
解答 证明:假设$\frac{1+x}{y}≥2,\frac{1+y}{x}≥2$.即 $\left\{\begin{array}{l}1+x≥2y\\ \\ 1+y≥2x\end{array}\right.$
∴2+x+y≥2x+2y
∴x+y≤2,这与x+y>2矛盾.
∴假设不成立
∴$\frac{1+x}{y},\frac{1+y}{x}$至少有一个小于2.
点评 本考点是反证法证明命题,在作证明题时,对于一些条件相对较少或者证明时需要分类讨论的题型,最好试试用反证法能否证明问题.对于有些题如本题,用反证法证明可以大大降低题目的解决难度.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
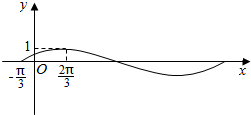
| A. | $ω=1,θ=\frac{π}{3}$ | B. | $ω=1,θ=-\frac{π}{3}$ | C. | $ω=\frac{1}{2},θ=\frac{π}{6}$ | D. | $ω=\frac{1}{2},θ=-\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${∫}_{-π}^{π}sinxdx=0$ | B. | $\int_{-\frac{π}{2}}^{\frac{π}{2}}{cos2xdx=\frac{1}{2}}$ | ||
| C. | ${∫}_{-\frac{π}{2}}^{\frac{π}{2}}cosxdx={2∫}_{0}^{\frac{π}{2}}cosxdx$ | D. | ${∫}_{0}^{1}\sqrt{x}dx=\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com