练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．用反证法证明命题：“三个连续正整数a，b，c中至少有一个能被2整除”时，要做的假设是（　　）
    A．假设三个连续正整数a，b，c都不能被2整除
    B．假设三个连续正整数a，b，c都能被2整除
    C．假设三个连续正整数a，b，c至多有一个能被2整除
    D．假设三个连续正整数a，b，c至多有两个能被2整除

    分析 写出要证明命题的否定，即为所求．

    解答 解：根据用反证法证明数学命题的步骤，应先假设要证命题的否定成立，
    而要证命题的否定为：“三个连续正整数a，b，c都不能被2整除”，
    故选：A．

    点评 本题主要考查用反证法证明数学命题的方法和步骤，求一个命题的否定，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．已知平面内n（n∈N+）条直线，任意两条都相交，任意三条不共点，这n条直线将平面分割成an个区域，则an=$\frac{{n}^{2}+n+2}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设X为随机变量，X～B （n，$\frac{1}{3}$），若随机变量X的数学期望E（X）=2，则P（X=2）等于（　　）
    A．$\frac{80}{243}$B．$\frac{13}{243}$C．$\frac{4}{243}$D．$\frac{13}{16}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．如图是某三棱锥的三视图，则该三棱锥的表面积为（　　）
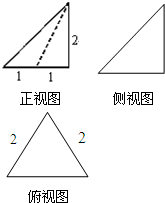
    A．4+$\sqrt{7}+\sqrt{3}$B．6+$\sqrt{7}$C．4+$\sqrt{7}$D．6+$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若A（-1，1），B（1，3），C（x，5），且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$，则实数λ等于（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知正项数列{an}的前n项和为Sn，数列{bn}的前n项和为Tn，且8Sn=（an+2）2，bn=$\frac{1}{2}$anλn-1（λ＞0，λ∈R）．
    （1）求数列{an}的通项公式；
    （2）求数列{bn}的前n项和Tn；
    （3）若不等式（1-λ）Tn+λbn≥2λn对任意的n∈N*恒成立，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

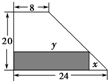    19．某厂有许多形状为直角梯形的铁皮边角料，如图，为降低消耗，开源节流，现要从这些边角料上截取矩形铁片（如图中阴影部分）备用，当截取的矩形面积最大时，矩形两边长x、y应为15，12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．在平面直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=2\sqrt{5}+t}\end{array}\right.$（t为参数），在极坐标系中（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴），曲线C1的极坐标方程为ρ=2．
    （Ⅰ）判断直线l与曲线C1的位置关系；
    （Ⅱ）已知曲线C2的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$（θ为参数），且M，N分别为曲线C2的上下顶点，点P为曲线C1上任意一点，试判断|PM|2+|PN|2是否为定值？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若（1-ax）6的展开式中的x3项的系数为20，则实数a=-1．

    查看答案和解析>>

    同步练习册答案