
| A. | ②③ | B. | ③④ | C. | ②③④ | D. | ①②④ |
分析 假设各函数为“控制增长函数”,根据定义推倒f(x+a)≤f(x)+b恒成立的条件,判断a,b的存在性即可得出答案.
解答 解:对于①,f(x+a)≤f(x)+b可化为:(x+a)2+(x+a)+1≤x2+x+1+b,
即2ax≤-a2-a+b,即x≤$\frac{-{a}^{2}-a+b}{2a}$对一切x∈R均成立,
由函数的定义域为R,故不存在满足条件的正常数a、b,故f(x)=x2+x+1不是“控制增长函数”;
对于②,若f(x)=$\sqrt{|x|}$是“控制增长函数”,则f(x+a)≤f(x)+b可化为:$\sqrt{|x+a|}$≤$\sqrt{|x|}$+b,
∴|x+a|≤|x|+b2+2b$\sqrt{|x|}$恒成立,又|x+a|≤|x|+a,
∴|x|+a≤|x|+b2+2b$\sqrt{|x|}$,∴$\sqrt{|x|}$≥$\frac{a-{b}^{2}}{2b}$,显然当a<b2时式子恒成立,
∴f(x)=$\sqrt{|x|}$是“控制增长函数”;
对于③,∵-1≤f(x)=sin(x2)≤1,∴f(x+a)-f(x)≤2,
∴当b≥2时,a为任意正数,使f(x+a)≤f(x)+b恒成立,故f(x)=sin(x2)是“控制增长函数”;
对于④,若f(x)=xsinx是“控制增长函数”,则(x+a)sin(x+a)≤xsinx+b恒成立,
∵(x+a)sin(x+a)≤x+a,∴x+a≤xsinx+b≤x+b,即a≤b,
∴f(x)=xsinx是“控制增长函数”.
故选C.
点评 本题考查了新定义的理解,函数存在性与恒成立问题研究,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
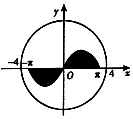 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x | B. | y=cosx | C. | y=${x^{\frac{2}{5}}}$ | D. | y=-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com