
分析 利用数量积大于零解出k的范围,去掉共线的特殊情况得答案.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=1×2×cos120°=-1.
∴($\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$+$\overrightarrow{b}$)=$k{\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}+{k}^{2}\overrightarrow{a}•\overrightarrow{b}+k{\overrightarrow{b}}^{2}$
=$k{\overrightarrow{a}}^{2}+({k}^{2}+1)\overrightarrow{a}•\overrightarrow{b}+k{\overrightarrow{b}}^{2}$=k-k2-1+4k=-k2+5k-1,
∵向量$\overrightarrow{a}$+k$\overrightarrow{b}$与k$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为锐角,
∴-k2+5k-1>0.解得$\frac{5-\sqrt{21}}{2}<k<\frac{5+\sqrt{21}}{2}$.
若向量$\overrightarrow{a}$+k$\overrightarrow{b}$与k$\overrightarrow{a}$+$\overrightarrow{b}$的方向相同,则$\overrightarrow{a}$+k$\overrightarrow{b}$=λ(k$\overrightarrow{a}$+$\overrightarrow{b}$),
即$\left\{\begin{array}{l}{λ=k}\\{k=1}\end{array}\right.$,∴k=1.
∴k的取值范围是($\frac{5-\sqrt{21}}{2},1$)∪(1,$\frac{5+\sqrt{21}}{2}$).
点评 本题考查了平面向量的数量积及夹角计算,注意共线的情况,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{193}$ | B. | 26 | C. | 17$\sqrt{2}$ | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | 2x-y-1=0 | C. | 2x+y+1=0 | D. | 2x+y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
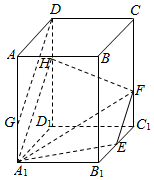 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E为B1C1的中点,F在CC1上,且C1F=1,G在AA1上,且AG=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{π}{2}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=$\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com