
分析 (Ⅰ)z为实数?m2+8m+15=0且m+5≠0,解得mj即可.
(Ⅱ)z为纯虚数?$\left\{\begin{array}{l}{\frac{{m}^{2}+m-6}{m+5}=0}\\{{m}^{2}+8m+15≠0}\end{array}\right.$,解出即可.
(III)z对应的点在第二象限?$\left\{\begin{array}{l}{\frac{{m}^{2}+m-6}{m+5}<0}\\{{m}^{2}+8m+15>0}\end{array}\right.$,解出即可.
解答 解:(Ⅰ)z为实数?m2+8m+15=0且m+5≠0,解得m=-3.
(Ⅱ)z为纯虚数?$\left\{\begin{array}{l}{\frac{{m}^{2}+m-6}{m+5}=0}\\{{m}^{2}+8m+15≠0}\end{array}\right.$,
解得m=2;
(III)z对应的点在第二象限?$\left\{\begin{array}{l}{\frac{{m}^{2}+m-6}{m+5}<0}\\{{m}^{2}+8m+15>0}\end{array}\right.$,
解得m<-5或-3<m<2.
点评 本题考查了复数为实数及纯虚数的充要条件、几何意义,考查了计算能力,属于基础题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | 8 | D. | ±8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
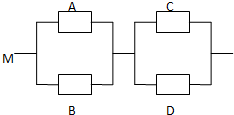 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{6\sqrt{10}}{10}$ | D. | $\frac{4\sqrt{10}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -360 | B. | 360 | C. | -60 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com