
分析 根据题意求出正△ABC的面积以及点O到底面的距离,再求出球的半径,即可求出球的表面积.
解答 解:正△ABC的三个顶点都在以O为球心的球面上,
且AB=AC=BC=2,
取BC中点D,连结AD,OD,
过O作OE⊥平面ABC,则OE∩AD=E,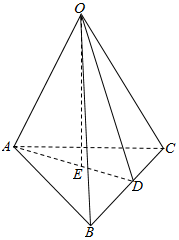 如图所示;
如图所示;
∴AD=$\sqrt{{2}^{2}{-1}^{2}}$=$\sqrt{3}$,
AE=$\frac{2}{3}$AD=$\frac{2\sqrt{3}}{3}$,
S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∵三棱锥O-ABC的体积为2,
∴$\frac{1}{3}$×$\sqrt{3}$×OE=2,
解得OE=2$\sqrt{3}$,
∴球的半径为OA=$\sqrt{{OE}^{2}{+AE}^{2}}$=$\sqrt{{(2\sqrt{3})}^{2}{+(\frac{2\sqrt{3}}{3})}^{2}}$=$\sqrt{\frac{40}{3}}$,
∴球的表面积为S=4π×OA2=$\frac{160π}{3}$.
故答案为:$\frac{160π}{3}$.
点评 本题考查了球的表面积求法问题,也考查了空间想象能力,是中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{8}^{4}$C${\;}_{4}^{2}$C${\;}_{2}^{2}$ | B. | C${\;}_{3}^{1}$C${\;}_{8}^{2}$ | ||
| C. | $\frac{{C}_{8}^{4}{C}_{4}^{2}}{{A}_{2}^{2}}$ | D. | $\frac{{C}_{8}^{4}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
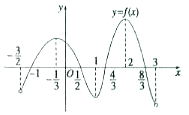 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x+2y+\sqrt{5}=0$或$x+2y-\sqrt{5}=0$ | B. | $x-2y+\sqrt{5}=0$或$x-2y-\sqrt{5}=0$ | ||
| C. | x+2y+5=0或x+2y-5=0 | D. | x-2y+5=0或x-2y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com