
分析 由二倍角的余弦函数公式化简cos2x,得到关于sinx的关系式,把sinx的值代入即可求出值,由sinx的值及x的范围,利用同角三角函数间的基本关系求出cosx的值,进而求出tanx的值,然后把所求的式子利用两角和的正切函数公式及特殊角的三角函数值化简后,将tanx的值代入即可求出值.
解答 解:由sinx=$\frac{3}{5}$,
得cos2x=1-2sin2x=$1-2×\frac{9}{25}=\frac{7}{25}$.
又sinx=$\frac{3}{5}$,$x∈(\frac{π}{2},π)$,
∴cosx=-$\frac{4}{5}$,
∴$tanx=\frac{sinx}{cosx}=-\frac{3}{4}$.
∴$tan(x+\frac{π}{4})$=$\frac{tanx+1}{1-tanx}=\frac{-\frac{3}{4}+1}{1+\frac{3}{4}}=\frac{1}{7}$.
点评 本题考查运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,灵活运用两角和的正切函数公式及特殊角的三角函数值化简求值,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
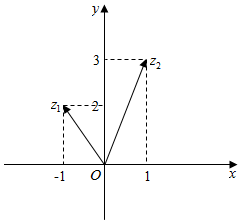 如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2
如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com