
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 从第二项起为等差数列 | D. | 从第二项起为等比数列 |
分析 由已知求得a2=1,再由数列递推式变形得到an+1=2an(n≥2),即$\frac{{{a_{n+1}}}}{a_n}=2(n≥2)$,验证$\frac{a_2}{a_1}=1$不满足上式,可得数列{an}从第二项起为等比数列.
解答 解:由a1=1,S2=2,得a2=S2-a1=2-1=1,
由Sn+1+2Sn-1=3Sn,得Sn+1-Sn=2(Sn-Sn-1)(n≥2),
即an+1=2an(n≥2),
∴$\frac{{{a_{n+1}}}}{a_n}=2(n≥2)$,
又$\frac{a_2}{a_1}=1$不满足上式,
∴数列{an}从第二项起为等比数列.
故选:D.
点评 本题考查数列递推式,考查了等比关系的确定,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1]∪(0,1) | C. | [-1,4] | D. | (-∞,-1]∪[0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
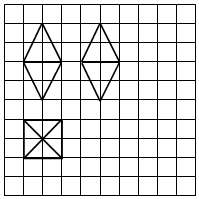 如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1个单位长度,图中粗线曲出的是某几何体的三视图,则该几何体的表面积为( )| A. | 16 | B. | 8$\sqrt{5}$ | C. | 32 | D. | 16$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
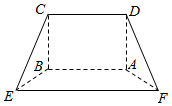 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 2 | 3 | 5 | 6 |
| 销售利润y(万元) | 5 | 7 | 9 | 11 |
| A. | $\hat b>0$ | B. | $\hat a>0$ | C. | 直线l过点(4,8) | D. | 直线l过点(2,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com