
分析 (Ⅰ)利用古典概型的概率公式,利用列举法进行求解即可;
(Ⅱ)利用几何概型的概率公式,求出对应的面积进行求解即可.
解答 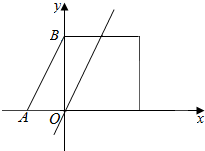 解:(Ⅰ) 设S≤1为事件A,x∈{-1,0,1,2},y∈{-1,0,1}
解:(Ⅰ) 设S≤1为事件A,x∈{-1,0,1,2},y∈{-1,0,1}
所以所有P(x,y)的所有可能点的集合列表表示为:
| -1 | 0 | 1 | |
| -1 | (-1,-1) | (-1,0) | (-1,1) |
| 0 | (0,-1) | (0,0) | (0,1) |
| 1 | (1,-1) | (1,0) | (1,1) |
| 2 | (2,-1) | (2,0) | (2,1) |
点评 本题主要考查古典概型和几何概型概率的计算,利用列举法以及转化法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
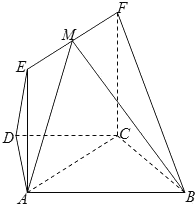 如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.
如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
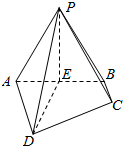 如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点
如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或$\frac{1}{4}$ | B. | $\frac{1}{2}$或$\frac{1}{8}$ | C. | 1或$\frac{1}{2}$ | D. | 1或$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
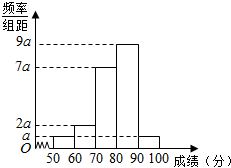 某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图
某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $({0,\frac{1}{2}})$ | C. | $({0,\frac{1}{4}})$ | D. | $({0,\frac{1}{8}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com