
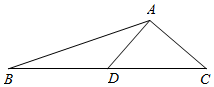
 已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.
已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.分析 (Ⅰ)由已知展开数量积,求出AB•AC的值,代入三角形面积公式得答案;
(Ⅱ)解法1:由AB=5,结合(Ⅰ)求得AC,延长AD到E,使AD=DE,连结BE,得到四边形ABEC为平行四边形,求出∠ABE=60°,设AD=x,则AE=2x,在△ABE中,由余弦定理求得x值得答案;
解法2:在△ABC中,由余弦定理得BC,再由正弦定理求得∠ACD的正弦值,进一步求得其余弦值,在△ADC中,利用余弦定理求得AD;
解法3:在△ABC中,由余弦定理得BC,在△ABC中,由余弦定理求出∠ACB,在△ADC中,由余弦定理求得AD.
解答 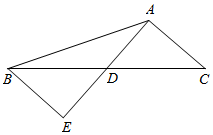 解:(Ⅰ)∵$\overrightarrow{AB}•\overrightarrow{AC}=-\frac{15}{2}$,
解:(Ⅰ)∵$\overrightarrow{AB}•\overrightarrow{AC}=-\frac{15}{2}$,
∴$AB•AC•cos∠BAC=-\frac{1}{2}AB•AC=-\frac{15}{2}$,
即AB•AC=15,
∴${S_{△ABC}}=\frac{1}{2}AB•ACsin∠BAC=\frac{1}{2}×15×\frac{{\sqrt{3}}}{2}=\frac{{15\sqrt{3}}}{4}$;
(Ⅱ)解法1:由AB=5,得AC=3,
延长AD到E,使AD=DE,连结BE,
∵BD=DC,
∴四边形ABEC为平行四边形,
∴∠ABE=60°,且BE=AC=3,
设AD=x,则AE=2x,在△ABE中,由余弦定理得:(2x)2=AB2+BE2-2AB•BEcos∠ABE=25+9-15=19,
解得$x=\frac{{\sqrt{19}}}{2}$,即AD的长为$\frac{{\sqrt{19}}}{2}$;
解法2:由AB=5,得AC=3,
在△ABC中,由余弦定理得:BC2=AB2+AC2-2AB•ACcos∠BAC=25+9+15=49,
得BC=7,
由正弦定理得:$\frac{BC}{sin∠BAC}=\frac{AB}{sin∠ACD}$,
得$sin∠ACD=\frac{ABsin∠BAC}{BC}=\frac{{5×\frac{{\sqrt{3}}}{2}}}{7}=\frac{{5\sqrt{3}}}{14}$,
∵0°<∠ACD<90°,
∴$cos∠ACD=\sqrt{1-{{sin}^2}∠ACD}=\frac{11}{14}$,
在△ADC中,$A{D^2}=A{C^2}+C{D^2}-2AC•CDcos∠ACD=9+\frac{49}{4}-2×3×\frac{7}{2}×\frac{11}{14}=\frac{19}{4}$,
解得$AD=\frac{{\sqrt{19}}}{2}$;
解法3:由AB=5,得AC=3,
在△ABC中,由余弦定理得:BC2=AB2+AC2-2AB•ACcos∠BAC=25+9+15=49,
得BC=7,
在△ABC中,$cos∠ACB=\frac{{A{C^2}+B{C^2}-A{B^2}}}{2AC•BC}=\frac{9+49-25}{2×3×7}=\frac{11}{14}$,
在△ADC中,由$A{D^2}=A{C^2}+C{D^2}-2AC•CDcos∠ACD=9+\frac{49}{4}-2×3×\frac{7}{2}×\frac{11}{14}=\frac{19}{4}$,
解得$AD=\frac{{\sqrt{19}}}{2}$.
点评 本题考查平面向量的数量积运算,考查了正弦定理和余弦定理在解三角形中的应用,是中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:选择题
| A. | a、b、c都是奇数 | |
| B. | a、b、c都是偶数 | |
| C. | a、b、c中至少有两个奇数 | |
| D. | a、b、c中至少有两个奇数或都是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆$\frac{{x}^{2}}{4}$+y2=1的右顶点为A,过椭圆长轴所在直线上的一个定点M(m,0)(不同于A)任作一条直线与椭圆相交于P、Q两点,直线AP、AQ的斜率分别记为k1、k2.
设椭圆$\frac{{x}^{2}}{4}$+y2=1的右顶点为A,过椭圆长轴所在直线上的一个定点M(m,0)(不同于A)任作一条直线与椭圆相交于P、Q两点,直线AP、AQ的斜率分别记为k1、k2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com