
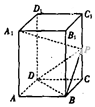
 如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.
如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.分析 (1)根据线面垂直的判定定理,要证BD⊥BD⊥A1P.,只证BD⊥AC,BD⊥AA1即可;
(2)以D为原点建立直角坐标系,则D(0,0,0),B(4,4,0),P(0,4,2$\sqrt{2}$),求出面PDB、面CDP的法向量即可.
解答 解:(1)证明:在长方体AC1中,连结A1C1,AC
∵底面ABCD是正方形,∴对角线BD⊥AC.
又∵A1A⊥平面ABCD,∴A1A⊥BD.
AC∩A1A=A,AC?面A1ACC1,A1A?面A1ACC1;
∴BD⊥面A1ACC1.∵A1P?面A1ACC1∴BD⊥A1P.
(2)如图以D为原点建立直角坐标系,则D(0,0,0)
B(4,4,0),P(0,4,2$\sqrt{2}$)
于是$\overrightarrow{BD}=(-4,-4,0)$,$\overrightarrow{PD}=(0,-4,-2\sqrt{2}$).
设$\overrightarrow{m}=(x,y,z)$是面PDB的法向量,由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BD}=-4x-4y=0}\\{\overrightarrow{m}•\overrightarrow{PD}=-4y-2\sqrt{2}z=0}\end{array}\right.$,
∴$\overrightarrow{m}=(\sqrt{2},-\sqrt{2},2)$.
面CDP的法向量为$\overrightarrow{n}=(1,0,0)$.
cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\sqrt{2}}{\sqrt{8}•1}=\frac{1}{2}$,∴二面角C-PD-B的余弦值为$\frac{1}{2}$.
点评 本题考查了空间异面直线垂直的证明方法,及向量法求二面角,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (5,6] | B. | (3,5) | C. | (3,6] | D. | [5,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.001的前提下,认为“数学成绩与物理成绩有关” | |
| B. | 在犯错误的概率不超过0.01的前提下,认为“数学成绩与物理成绩有关” | |
| C. | 有99%以上的把握认为“数学成绩与物理成绩无关” | |
| D. | 有99.9%以上的把握认为“数学成绩与物理成绩有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2{e^2}}}$ | B. | $\frac{1}{2}{e^2}$ | C. | $\frac{1}{e}$ | D. | $-\frac{3}{{2{e^2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
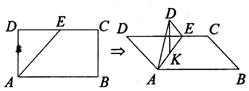 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com