
分析 设圆O1及与圆O2的半径分别为r1,r2,运用圆与圆的位置关系和圆的面积公式进行求解.
解答 设圆O1及与圆O2的半径分别为r1,r2,
则$\left\{\begin{array}{l}{(r-{r}_{1})sinθ={r}_{1}}\\{({r}_{1}+{r}_{2})cos(\frac{π}{2}-θ)={r}_{1}-{r}_{2}}\end{array}\right.$,得:$\left\{\begin{array}{l}{{r}_{1}=\frac{rsinθ}{1+sinθ}}\\{{r}_{2}=\frac{{r}_{1}(1-sinθ)}{1+sinθ}}\end{array}\right.$
∴${r}_{2}=\frac{rsinθ(1-sinθ)}{(1+sinθ)^{2}}$,
∵0<2θ<2π,
∴0<θ<π,
令t=1+sinθ,(1<t<2).
那么:${r}_{2}=\frac{-{t}^{2}+3t-2}{{t}^{2}}$=$-2(\frac{1}{t}-\frac{3}{4})^{2}+\frac{1}{8}$,
当$\frac{1}{t}=\frac{4}{3}$,即sinθ=$\frac{1}{3}$时,圆O2的半径最大,圆O2的面积最大,
最大值是$\frac{{r}^{2}π}{64}$.
点评 本题考查了圆与圆的关系式问题,正确掌握圆与圆的位置关系是准确解题的关键.属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
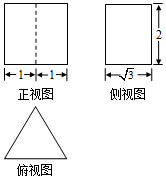
| A. | 12 | B. | 8+2$\sqrt{3}$ | C. | 12+2$\sqrt{3}$ | D. | 12+4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学成绩 | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| 物理成绩 | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com