
分析 日语和韩语都要求必须有女生参加.先从三个女生中选一个考日语,再从剩下的女生中选一个考韩语,剩下的三个考生在三个位置排列,去掉重复部分,即当考日语的和韩语的有两个女生.
解答 解:∵由题意知日语和韩语都要求必须有女生参加考试,
∴先从三个女生中选一个考日语有3种结果,
再从剩下的女生中选一个考韩语有2种结果,
剩下的三个考生在三个位置排列A33种结果,
这样重复一部分,考日语的和韩语的有两个女生时2A33种结果,
∴共有C31C21A33-2A33=24.
故答案为:24
点评 本题考查了分类和分步计数原理,分类要做到“不重不漏”.分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.分步要做到“步骤完整”--完成了所有步骤,恰好完成任务.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | [-1,3] | C. | (-∞,1] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
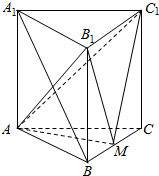 如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com