
| A. | 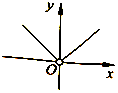 | B. |  | C. |  | D. | 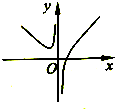 |
分析 讨论a的范围,利用导数判断f(x)的单调性得出答案.
解答 解:f(x)=$\left\{\begin{array}{l}{x-\frac{a}{x},x>0}\\{-x-\frac{a}{x},x<0}\end{array}\right.$,∴f′(x)=$\left\{\begin{array}{l}{1+\frac{a}{{x}^{2}},x>0}\\{-1+\frac{a}{{x}^{2}},x<0}\end{array}\right.$.
(1)当a=0时,f(x)=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$,图象为A;
(2)当a>0时,1+$\frac{a}{{x}^{2}}$>0,∴f(x)在(0,+∞)上单调递增,
令-1+$\frac{a}{{x}^{2}}$=0得x=-$\sqrt{a}$,∴当x<-$\sqrt{a}$时,-1+$\frac{a}{{x}^{2}}$<0,当-$\sqrt{a}$<x<0时,-1+$\frac{a}{{x}^{2}}$>0,
∴f(x)在(-∞,-$\sqrt{a}$)上单调递减,在(-$\sqrt{a}$,0)上单调递增,图象为D;
(3)当a<0时,-1+$\frac{a}{{x}^{2}}$<0,∴f(x)在(-∞,0)上单调递减,
令1+$\frac{a}{{x}^{2}}$=0得x=$\sqrt{-a}$,∴当x>$\sqrt{-a}$时,1+$\frac{a}{{x}^{2}}$>0,当0<x<$\sqrt{-a}$时,1+$\frac{a}{{x}^{2}}$<0,
∴f(x)在(0,$\sqrt{-a}$)上单调递减,在($\sqrt{-a}$,+∞)上单调递增,图象为B;
故选C.
点评 本题考查了导数与函数单调性的关系,分类讨论思想,属于中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
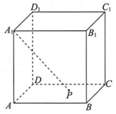 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足A1P≥$\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 偏爱微信 | 偏爱QQ | 合计 | |
| 30岁以下 | 4 | 8 | 12 |
| 30岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| A. | 在犯错误的概率不超过0.005的前提下认为社交软件使用习惯与年龄有关 | |
| B. | 在犯错误的概率超过0.005的前提下认为社交软件使用习惯与年龄有关 | |
| C. | 在犯错误的概率不超过0.001的前提下认为社交软件使用习惯与年龄有关 | |
| D. | 在犯错误的概率超过0.001的前提下认为社交软件使用习惯与年龄有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | $-\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可以不存在 | B. | 至少有1个 | C. | 至少有2个 | D. | 至多有2个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com