
分析 画出y=cosx一个周期的图象,化简不等式后由余弦函数的图象和周期性,求出不等式的解集.
解答 解: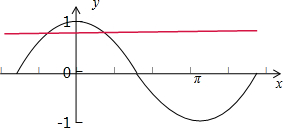 由2cos($\frac{x}{2}$-$\frac{π}{4}$)>$\sqrt{3}$得,
由2cos($\frac{x}{2}$-$\frac{π}{4}$)>$\sqrt{3}$得,
cos($\frac{x}{2}$-$\frac{π}{4}$)>$\frac{\sqrt{3}}{2}$,画出y=cosx一个周期的图象,
所以由图得,$-\frac{π}{6}+2kπ<\frac{x}{2}-\frac{π}{4}<\frac{π}{6}+2kπ,k∈Z$,
解得$\frac{π}{6}+4kπ<x<\frac{5π}{6}+4kπ,k∈Z$,
所以不等式的解集是$(\frac{π}{6}+4kπ,\frac{5π}{6}+4kπ),k∈Z$.
点评 本题考查利用余弦函数的图象和周期性求不等式的解集,考查数形结合思想.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2016}$ | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意的x∈R,log2x<0 | B. | 对任意的x∈R,log2x≥0 | ||
| C. | 不存在x∈R,log2x≥0 | D. | 存在x0∈R,log2x0≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
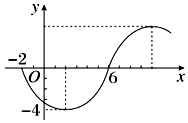
| A. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | B. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | C. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [25,35) | [35,45) | [4,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 甲厂频数 | 10 | 40 | 115 | 165 | 120 | 45 | 5 |
| 乙厂频数 | 5 | 60 | 110 | 160 | 90 | 70 | 5 |
| P(k2≥k) | 0.05 | 0.01 | 0.001 |
| h | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
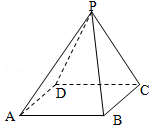 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )| A. | 4 | B. | 8 | C. | 12π | D. | 16π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com