
分析 (1)方式一中随机变量ξ可取的值为0,1,2,且ξ服从超几何分布ξ~H(2,3,10),计算对应的概率;列出频率分布表;方式二中随机变量ξ可取的值为0,1,2,且ξ服从二项分布ξ~B(2,$\frac{3}{10}$),计算对应的概率;列出频率分布表;
(2)计算方式一与方式二中的数学期望(平均数),比较结果即可.
解答 解:(1)方式一中随机变量ξ可取的值为0,1,2,且ξ服从超几何分布,ξ~H(2,3,10),
于是P(ξ=0)=$\frac{{C}_{3}^{0}{•C}_{7}^{2}}{{C}_{10}^{2}}$=$\frac{7}{15}$;P(ξ=1)=$\frac{{C}_{3}^{1}{•C}_{7}^{1}}{{C}_{10}^{2}}$=$\frac{7}{15}$;P(ξ=2)=$\frac{{C}_{3}^{2}{•C}_{7}^{0}}{{C}_{10}^{2}}$=$\frac{1}{15}$;
因此ξ的频率分布可表示为下表:
| ξ | 0 | 1 | 2 |
| P | $\frac{7}{15}$ | $\frac{7}{15}$ | $\frac{1}{15}$ |
| ξ | 0 | 1 | 2 |
| P | $\frac{49}{100}$ | $\frac{21}{50}$ | $\frac{9}{100}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的应用问题,是中档题目.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
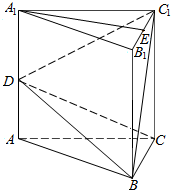 三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.
三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-4)2+(y-5)2=10 | B. | (x+4)2+(y-5)2=10 | C. | (x-4)2+(y+5)2=10 | D. | (x+4)2+(y+5)2=10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com