
分析 (1)把直线与双曲线方程联立消去y,利用二次项非0,且判别式大于0求得a的范围.
(2)求出双曲线C的右焦点为($\frac{2\sqrt{3}}{3}$,0),双曲线的渐近线方程,可得圆的半径,即可求出圆的方程.
解答 解:(1)直线1:y=ax+1与双曲线C,得(3-a2)x2-2ax-2=0
∵直线l与曲线C有两个交点A、B,
∴$\left\{\begin{array}{l}{3-{a}^{2}≠0}\\{4{a}^{2}-4(3-{a}^{2})×(-2)>0}\end{array}\right.$.
∴实数a的取值范围是-$\sqrt{6}$<a<$\sqrt{6}$且a$≠±\sqrt{3}$;
(2)双曲线C的右焦点为($\frac{2\sqrt{3}}{3}$,0),双曲线的渐近线方程为y=±$\sqrt{3}$x,
圆心到双曲线的渐近线的距离d=$\frac{2}{\sqrt{3+1}}$=1,
∴以双曲线C的右焦点为圆心且与双曲线的渐近线相切的圆C1的方程为(x-$\frac{2\sqrt{3}}{3}$)2+y2=1.
点评 本题主要考查了双曲线的简单性质,直线与双曲线的位置关系.考查了学生综合分析问题和推理的能力,基本的运算能力.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | [2,+∞) | C. | (-∞,2] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知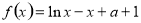 .
.
(1)若存在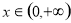 使得
使得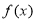 ≥0成立,求
≥0成立,求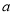 的范围;
的范围;
(2)求证:当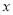 >1时,在(1)的条件下,
>1时,在(1)的条件下,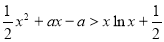 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-eln2)∪(eln2,2] | B. | [-eln2,0)∪(0,eln2] | C. | [-2,0)∪(0,2] | D. | [-e,-2)∪(2,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com