考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)取BC中点O,连结AO,由已知条件得AO⊥BC,平面ABC⊥平面BCC
1B
1,以O为原点,
,,的方向为x,y,z轴的正方向,建立空间直角坐标系,利用向量法能求出二面角B
1-BD-A
1的余弦值.
(2)由
=(1,2,-
)为平面A
1BD的法向量,
=(0,1,0),利用向量法能求出C
1点到A
1BD的距.
解答:
解:(1)取BC中点O,连结AO,
∵△ABC为正三角形,∴AO⊥BC.
∵在正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面BCC
1B
1,
∴AO⊥平面BCC
1B
1.
取B
1C
1中点O
1,以O为原点,
,,的方向为x,y,z轴的正方向,
建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),A
1(0,2,
),
A(0,0,
),B
1(1,2,0),C
1(-1,2,0)
∴
=(1,2,-),=(-2,1,0),=(-1,2,).
∴
•=0,•=0∴
⊥,⊥,∴AB
1⊥平面BDA
1.
即
=(1,2,-
)为平面BDA
1的法向量.
取平面B
1BD的一个法向量为
=(0 ,0 ,),
cos<,>===-.
∴二面角B
1-BD-A
1的余弦值为
.
(2)∵
=(1,2,-
)为平面A
1BD的法向量,
=(0,1,0)
∴C
1点到平面A
1BD的距离为:
d=||=||==.
点评:本题考查二面角的余弦值的求法,考查点到平面的距离的求法,解题时要认真审题,注意向量法的合理运用.

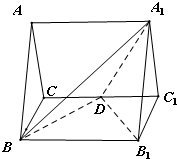
 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. ∵△ABC为正三角形,∴AO⊥BC.
∵△ABC为正三角形,∴AO⊥BC.

 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=2 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.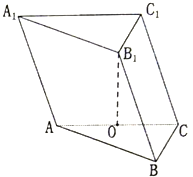 已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.
已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.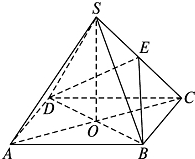 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.