
分析 (1)由已知条件推导出$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,由此能求出椭圆C的方程.
(2)假设存在这样的点P(x0,y0),设出直线AP的方程和直线BP的方程,由直线AP,BP分别与直线x=3交于点M,N,得△PMN的面积=$\frac{|{x}_{0}+{y}_{0}|(3-{x}_{0})^{2}}{|{{x}_{0}}^{2}-1|}$,△PAB的面积=|x0+y0|,由此能确定存在点P使得△PAB和△△PMN的面积相等,并能求出点P坐标.
解答 解:(1)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(-1,1),离心率为$\frac{\sqrt{6}}{3}$,
∴$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=4,b2=$\frac{4}{3}$,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}$=1.
(2)如图,假设存在这样的点P(x0,y0),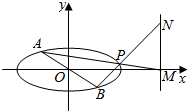
因为A(-1,1),B(1,-1),
则直线AP的方程为y-1=$\frac{{y}_{0}-1}{{x}_{0}+1}$(x+1),
直线BP的方程为y+1=$\frac{{y}_{0}+1}{{x}_{0}-1}$(x-1),
∵直线AP,BP分别与直线x=3交于点M,N,
∴令x=3,得yM=$\frac{4{y}_{0}+{x}_{0}-3}{{x}_{0}+1}$,yN=$\frac{2{y}_{0}-x+3}{{x}_{0}-1}$,
∴△PMN的面积S△PMN=$\frac{1}{2}$|yM-yN|(3-x0)=$\frac{|{x}_{0}+{y}_{0}|(3-{x}_{0})^{2}}{|{{x}_{0}}^{2}-1|}$,
又∵AB=2$\sqrt{2}$,直线AB的方程为x+y=0,
∴点P到直线AB的距离d=$\frac{|{x}_{0}+{y}_{0}|}{\sqrt{2}}$,
∴△PAB的面积S△PAB=$\frac{1}{2}AB•d$=|x0+y0|,
∵点P不同于A,B,∴|x0+y0|≠0,
∴(3-x0)2=|x02-1|
解得x0=$\frac{5}{3}$,从而y0=±$\frac{\sqrt{33}}{9}$,
∴存在点P使得△PAB和△△PMN的面积相等,点P坐标为($\frac{5}{3}$,±$\frac{\sqrt{33}}{9}$).
点评 本题考查椭圆方程的求法,考查满足条件的点是否存在的确定,综合性强,难度大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
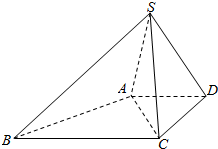 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
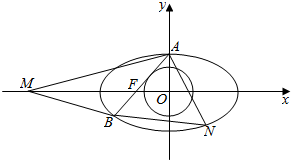 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=$\frac{{b}^{2}}{2}$,椭圆C1短轴的上端点为A,左焦点为F,直线AF与圆C2相切,椭圆C1左焦点到左准线的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 与点P的位置有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
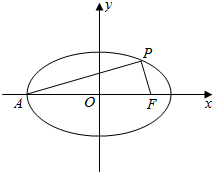 如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点且PA⊥PF.
如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点且PA⊥PF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com