
| A. | f(x)=$\root{3}{{x}^{3}}$与$g(x)=\sqrt{x^2}$ | B. | f(x)=|x|与$g(x)={({\sqrt{x}})^2}$ | ||
| C. | $f(x)=\sqrt{1-x}×\sqrt{1+x}$与$g(x)=\sqrt{1-{x^2}}$ | D. | f(x)=x0与g(x)=1 |
分析 根据两个函数是同一个函数的定义,函数的三要素均相等,或两个函数的图象一致,根据函数的定义域与函数的解析式一致时,函数的值域一定相同,我们逐一分析四个答案中两个函数的定义域和解析式是否一致,即可得到答案.
解答 解:对于A:f(x)=x,g(x)=|x|,不是同一函数,
对于B:f(x)的定义域是R,g(x)的定义域是[0,+∞),不是同一函数,
对于C:f(x)=g(x),表达式相同,定义域都是[-1,1],是同一函数,
对于D:f(x)的定义域是{x|x≠0},g(x)的定义域是R,不是同一函数,
故选:C.
点评 本题考查的知识点是判断两个函数是否为同一函数,熟练掌握判断两个函数是否为同一函数的方法,正确理解两个函数表示同一函数的概念是解答本题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | (-1,1] | D. | [-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
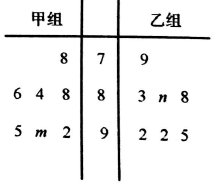 某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )
某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0$<\frac{r}{L}<\frac{1}{2}$ | B. | $\frac{1}{2}≤\frac{r}{L}<1$ | C. | 0$<\frac{r}{L}<\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}≤\frac{r}{L}<1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com