
分析 (1)由题意可得-1≤x2-1≤2,解得x的范围,即可求得函数f(x2-1)的定义域;
(2)由已知中函数f(3x-4)的定义域为[0,4),我们可以求出函数f(x)的定义域,进而求出函数f(1-2x)的定义域.
解答 解:(1)∵函数f(x)的定义域为(-1,2],
∴-1<x2-1≤2,解得:-$\sqrt{3}$≤x≤$\sqrt{3}$,且x≠0,
故函数的定义域是[-$\sqrt{3}$,0)∪(0,$\sqrt{3}$];
(2)∵0≤x<4,
∴-4≤3x-4<8,
∴-4≤1-2x<8,
∴-$\frac{7}{2}$<x≤$\frac{5}{2}$,
故函数的定义域是(-$\frac{7}{2}$,$\frac{5}{2}$].
点评 本题考查的知识点是函数的定义域及其求法,其中熟练掌握抽象函数定义域求解时“一不变(括号里整体的取值范围不变),应万变”的原则是解答此类问题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
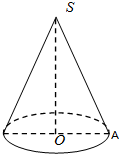 如图,课桌上放着一个圆锥SO,点A为圆锥底面圆周上一点,SA=2cm,OA=1cm,蚂蚁从点A沿圆锥的侧面爬行一周再回到A,则蚂蚁行迹的最短路程是( )
如图,课桌上放着一个圆锥SO,点A为圆锥底面圆周上一点,SA=2cm,OA=1cm,蚂蚁从点A沿圆锥的侧面爬行一周再回到A,则蚂蚁行迹的最短路程是( )| A. | 2πcm | B. | 2$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com