
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
分析 由题意得1-cosAcosB-cos2$\frac{C}{2}$=0,化简可得cos(A-B)=0,根据-π<A-B<π,求得A-B=0,从而得到结论.
解答 解:∵关于x的方程x2-xcosAcosB-cos2$\frac{C}{2}$=0有一个根为1,
∴1-cosAcosB-cos2$\frac{C}{2}$=0,即sin2$\frac{C}{2}$=cosAcosB,
∴$\frac{1-cosC}{2}$=cosAcosB,
∴1=2cosAcosB-cos(A+B)=cosAcosB+sinAsinB=cos(A-B),
∵-π<A-B<π,
∴A-B=0,即:A=B,故△ABC一定是等腰三角形,
故选:A.
点评 本题考查两角和差的余弦公式的应用,求出cos(A-B)=0,及-π<A-B<π,是解题的关键,属于基础题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
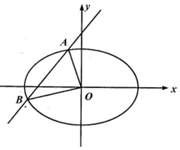 如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.
如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
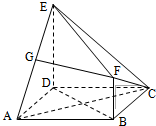 在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.
在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
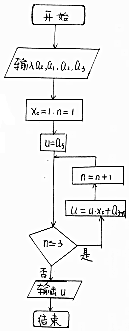 如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com