
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设D1在平面ABC的射影为E,连接D1E,根据线面垂直的性质与判定,面面垂直的判定定理寻找互相垂直的平面.
解答 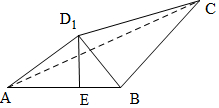 解:设D1在平面ABC的射影为E,连接D1E,则D1E⊥平面ABC,
解:设D1在平面ABC的射影为E,连接D1E,则D1E⊥平面ABC,
∵D1E?平面ABD1,∴平面ABD1⊥平面ABC.
∵D1E⊥平面ABC,BC?平面ABC,
∴D1E⊥BC,又AB⊥BC,D1E∩AB=E,
∴BC⊥平面ABD1,又BC?平面BCD1,
∴平面BCD1⊥平面ABD1,
∵平面BC⊥平面ABD1,AD1?平面ABD1,
∴BC⊥AD1,又CD1⊥AD1,BC∩CD1=C,
∴AD1⊥平面BCD1,又AD1?平面ACD1,
∴平面ACD1⊥平面BCD1.
∴共有3对平面互相垂直.
故选:B.
点评 本题考查了线面垂直的性质与判定,面面垂直的判定,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{6}$ | B. | $\frac{25}{8}$ | C. | $\frac{25}{3}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 10 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
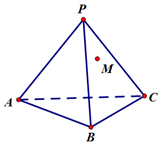 如图,正三棱锥P-ABC,已知AB=2,PA=3
如图,正三棱锥P-ABC,已知AB=2,PA=3查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com