
| A. | 1 | B. | 10 | C. | 5 | D. | 8 |
分析 判定函数f(x)是定义域R上的奇函数,且为单调减函数,
把不等式f(a2-2a)+f(2b-b2)≤0化为a2-2a≥-2b+b2,
即(a+b-2)(a-b)≥0,再由1≤a≤4得出不等式组,
画出不等式组表示的平面区域即可行域,
利用目标函数Z=2a-b,求出Z的最大值即可.
解答 解:函数$f(x)=ln({\sqrt{{x^2}+1}-x})$,定义域为R,且对于任意的x∈R都有
f(-x)+f(x)=ln($\sqrt{{(-x)}^{2}+1}$+x)+ln($\sqrt{{x}^{2}+1}$-x)=ln(x2+1-x2)=0,
∴函数y=f(x)定义域R上的为奇函数;
由f(a2-2a)+f(2b-b2)≤0可得f(a2-2a)≤-f(2b-b2)
由函数为奇函数可得式f(a2-2a)≤f(-2b+b2);
又∵f′(x)=$\frac{\frac{x}{\sqrt{{x}^{2}+1}}-1}{\sqrt{{x}^{2}+1}-x}$<0恒成立,
∴函数f(x)为R上的减函数;
∴a2-2a≥-2b+b2,即a2-b2-2(a-b)≥0,
整理可得,(a+b-2)(a-b)≥0,
作出不等式组$\left\{\begin{array}{l}{(a+b-2)(a-b)≥0}\\{1≤a≤4}\end{array}\right.$
所表示的平面区域即可行域如图所示的△ABC;
令Z=2a-b,则Z表示2a-b-Z=0在y轴上的截距的相反数,
由图可知,当直线经过点A(1,1)时Z最小,最小值为Z=2×1-1=1,
当直线经过点C(4,-2)时Z最大,最大值为2×4-(-2)=10.
故选:B.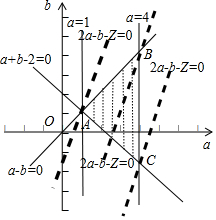
点评 本题主要考查了复合函数的单调性与奇偶性的综合应用问题,也考查了不等式表示平面区域的确定,以及用线性规划求目标函数的最值问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,在四面体D1ABC的四个面中,其中有n对平面相互垂直,则n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ef(1)<f(2) | B. | f(1)<0 | C. | ef(e)<2f(2) | D. | f(1)<2ef(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
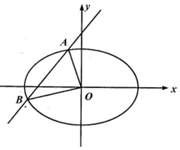 如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.
如图,设斜率为k(k>0)的直线l与椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点,且OA⊥OB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
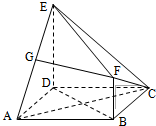 在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.
在多面体ABCDEF中,四边形ABCD为正方形,AD=DE=2BF=2,ED⊥平面ABCD,FB∥ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com