
|
| A、{-3,0} |
| B、{3,-1} |
| C、{0,1} |
| D、{-3,0,1} |



科目:高中数学 来源: 题型:
| 性别 中国政府是否 需要在钓鱼岛和其他争议 问题上持续对日强硬 |
男 | 女 |
| 需要 | 50 | 250 |
| 不需要 | 100 | 150 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“?x∈R,2x>0”的否定是“?x0∈R,2x0≤0” | ||||
| B、命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | ||||
C、“sinα=
| ||||
| D、函数y=2x-3+1的图象恒过定点A(3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0 |
| B、命题“矩形是平行四边形”的否定为真命题 |
| C、命题“若cosx=cosy,则x=y”的逆否命题为真命题 |
| D、命题“若x+y=0,则x,y互为相反数”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、命题“存在x∈R,x2-x>0”的否定是“对任意x∈R,x2-x<0”. |
| B、设α,β为两个不同的平面,直线l?α,则“l⊥β”是“α⊥β”成立的必要不充分条件. |
| C、命题“若a<b,则am2<bm2”的否命题是真命题. |
| D、已知x∈R,则“x>1”是“x>2”的充分不必要条件. |
查看答案和解析>>
科目:高中数学 来源: 题型:
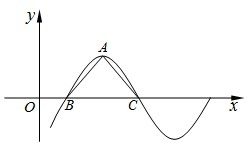 已知函数f(x)=
已知函数f(x)=| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com