考点:棱柱的结构特征,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:对于①,根据MN?平面A
1C
1CA,可以通过判断BD是否垂直于平面A
1C
1CA而得出结论.
对于②,先证AC
1⊥平面A
1BD,再将A
1C平移至MN,即可探究点N的存在性.
对于③,根据两异面直线所成角的定义,作出平面角,将此平面角放在一个三角形中,设出正方体中的相关量,解此三角形,列出余弦值的表达式,可得余弦值的范围,即可判断
是否在此范围内.
对于④,根据
VB-MND1=VN-BMD1,考虑三棱锥
VN-BMD1的底面积与高,即可知三棱锥B-MND
1的体积是否为定值.
解答:
解:在①中,连接A
1C
1,由正方体的几何特征知,B
1D
1⊥A
1C
1,B
1D
1⊥AA
1,
∴B
1D
1⊥平面ACC
1A
1,又MN?平面ACC
1A
1,∴B
1D
1⊥MN,
故①正确.
在②中,连接AC
1,由正方体的几何特征知,AC
1⊥A
1B,AC
1⊥A
1D,
∴AC
1⊥平面A
1BD.
当N是棱CC
1的中点时,MN∥AC
1,则MN∥平面A
1BD.
故②正确.
在③中,过N作CD的平行线NE,交DD
1于E,连接ME,
过M作MF⊥EN交NE于F,则∠FNM即为异面直线MN与A
1B
1所成的角.如右图所示.
由
知,Rt△EDM≌Rt△NCM,
∴ME=MN,∴EF=FN.
设正方体的棱长为2,CN=x,则cos∠FNM=
=,
由0≤x≤2知,
≤cos∠FNM≤
,
而
∉[,],故③错误.
在④中,考虑△D
1BM,以BM为底,DD
1为高,可知
S△MBD1是定值.
又CC
1∥平面BB
1D
1D,∴N到平面BB
1D
1D的距离等于CC
1到平面BB
1D
1D的距离,为定值,
∴三棱锥N-BMD
1的体积为定值,
由
VB-MND1=VN-BMD1知,三棱锥B-MND
1的体积为定值,
故④正确.
综上,正确命题是①②④.
故答案为①②④.
点评:本题考查立体几何的综合应用,推理论证能力,分析问题、解决问题的能力.解题的关键在于熟练应用定义、定理及性质等.

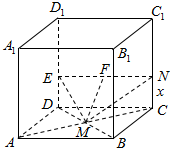
 如图所示,在正方体ABCD-A1B1C1D1中,M是正方形ABCD的中心,N是棱CC1(包括端点)上的动点,现给出以下命题:
如图所示,在正方体ABCD-A1B1C1D1中,M是正方形ABCD的中心,N是棱CC1(包括端点)上的动点,现给出以下命题:


 高中必刷题系列答案
高中必刷题系列答案