
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)求出f($\frac{1}{{e}^{a}}$)的解析式,根据函数的单调性判断即可;
(Ⅲ)根据函数的单调性求出f(x)的最大值,得到关于a的不等式,求出a的范围即可.
解答 解:(Ⅰ)∵g(x)=2x-ex,∴x∈R,且g′(x)=2x-ex.
∴当x<ln2时,g′(x)>0,g(x)单调递增,
当x>ln2时,g′(x)<0,g(x)单调递减,
所以函数g(x)的单调递增区间是(-∞,ln2],单调递减区间是[ln2,+∞).…(2分)
(Ⅱ)∵f(x)=1-$\frac{1}{x}$-alnx,∴f($\frac{1}{{e}^{a}}$)=1-ea+a2(a>1).
设h(x)=1-ex+x2,∴h′(x)=-ex+2x.
由(Ⅰ)知,当x>1时,h′(x)<h′(1)=2-e<0,
h(x)在区间[1,+∞)单调递减,
∴x>1时,h(x)<h(1)=-e<0.
∴a>1时,f($\frac{1}{{e}^{a}}$)<0,即f($\frac{1}{{e}^{a}}$)符号是“-”.…(5分)
(Ⅲ)由函数f(x)=1-$\frac{1}{x}$-alnx得,x>0且f′(x)=$\frac{1-ax}{{x}^{2}}$.
当a≤0时,f′(x)>0,f(x)单调递增,f(x)没有两个零点,∴a>0…(6分)
∴f′(x)=-$\frac{a}{{x}^{2}}$(x-$\frac{1}{a}$).∴当0<x<$\frac{1}{a}$时,f′(x)>0,f(x)单调递增.
当x>$\frac{1}{a}$时,f′(x)<0,f(x)单调递减.又f′($\frac{1}{a}$)=0,
∴f(x)max=f($\frac{1}{a}$)=1-a+alna.…(7分)
设s(x)=1-x+xlnx,∴x>0且s′(x)=lnx,同上可得s(x)min=s(1)=0,
∴当a>0且a≠1时,f(x)max>0,当a=1时,f(x)没有两个零点.…(8分)
设t(x),则t′(x)=ex-1,∴x>1时,t′(x)>0,t(x)单调递增,
所以x>1时,t(x)>t(1),即x>1时,ex>x.…(9分)
当a>1时,ex>a,∴$\frac{1}{{e}^{x}}$<$\frac{1}{a}$<1.∵f($\frac{1}{{e}^{x}}$),
∴f(x)在区间($\frac{1}{{e}^{x}}$,$\frac{1}{a}$)上有一个零点,又f(1)=0,
∴f(x)有两个零点.…(10分)
当0<a<1时,1<$\frac{1}{a}$<${e}^{\frac{1}{a}}$.∵f(${e}^{\frac{1}{a}}$)=-${e}^{-\frac{1}{a}}$<0,
∴f(x)在区间($\frac{1}{a}$,${e}^{\frac{1}{a}}$)上有一个零点,
又f(1)=0,∴f(x)有两个零点.…(11分)
综上所述,实数a的取值范围是(0,1)∪(1,+∞).…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
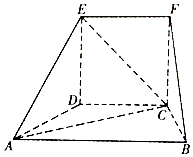 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAC=30°,AC⊥FB.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAC=30°,AC⊥FB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
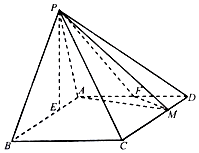 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,AD=2$\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com