
 某公路段在某一时刻内监测到的车速频率分布直方图如图所示.
某公路段在某一时刻内监测到的车速频率分布直方图如图所示.分析 (1)由频率分布直方图中所有小长形面积之和为1,能求出h=0.01,由此能求出第三个小长方形的面积.
(2)利用频率分布直方图能求出平均车速$\overline v$的估计值.
解答 解:(1)∵频率分布直方图中所有小长形面积之和为1,
∴10h+10×3h+10×4h+10×2h=1,
解得h=0.01,…(3分)
∴第三个小长方形的面积为:10×4h=10×0.04=0.4…(5分)
(2)由频率分布直方图得:
平均车速$\overline v$=0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.…(10分)
点评 本题考查频率分布直方图等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内心 | B. | 外心 | C. | 垂心 | D. | 重心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 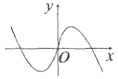 | B. | 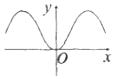 | C. | 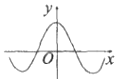 | D. | 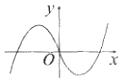 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{15}$ | B. | $\frac{2}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com