
分析 (Ⅰ)设椭圆的离心率为e.通过$\frac{1}{2}(c+a)c=\frac{b^2}{2}$.转化求解椭圆的离心率.
(Ⅱ)(ⅰ)依题意,设直线FP的方程为x=my-c(m>0),则直线FP的斜率为$\frac{1}{m}$.通过a=2c,可得直线AE的方程为$\frac{x}{2c}+\frac{y}{c}=1$,求解点Q的坐标为$(\frac{(2m-2)c}{m+2},\frac{3c}{m+2})$.利用|FQ|=$\frac{3c}{2}$,求出m,然后求解直线FP的斜率.
(ii)求出椭圆方程的表达式你,求出直线FP的方程为3x-4y+3c=0,与椭圆方程联立通过$|FP|=\sqrt{{{(c+c)}^2}+{{(\frac{3c}{2})}^2}}=\frac{5c}{2}$,结合直线PM和QN都垂直于直线FP.结合四边形PQNM的面积为3c,求解c,然后求椭圆的方程.
解答 解:(Ⅰ)设椭圆的离心率为e.由已知,可得$\frac{1}{2}(c+a)c=\frac{b^2}{2}$.又由b2=a2-c2,可得2c2+ac-a2=0,即2e2+e-1=0.又因为0<e<1,解得$e=\frac{1}{2}$.
所以,椭圆的离心率为$\frac{1}{2}$;
(Ⅱ)(ⅰ)依题意,设直线FP的方程为x=my-c(m>0),则直线FP的斜率为$\frac{1}{m}$.
由(Ⅰ)知a=2c,可得直线AE的方程为$\frac{x}{2c}+\frac{y}{c}=1$,即x+2y-2c=0,与直线FP的方程联立,可解得$x=\frac{(2m-2)c}{m+2},y=\frac{3c}{m+2}$,即点Q的坐标为$(\frac{(2m-2)c}{m+2},\frac{3c}{m+2})$.
由已知|FQ|=$\frac{3c}{2}$,有${[\frac{(2m-2)c}{m+2}+c]^2}+{(\frac{3c}{m+2})^2}={(\frac{3c}{2})^2}$,整理得3m2-4m=0,所以$m=\frac{4}{3}$,即直线FP的斜率为$\frac{3}{4}$.
(ii)解:由a=2c,可得$b=\sqrt{3}c$,故椭圆方程可以表示为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$.
由(i)得直线FP的方程为3x-4y+3c=0,与椭圆方程联立$\left\{\begin{array}{l}3x-4y+3c=0\\ \frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1\end{array}\right.$消去y,整理得7x2+6cx-13c2=0,解得$x=-\frac{13c}{7}$(舍去),或x=c.因此可得点$P(c,\frac{3c}{2})$,进而可得$|FP|=\sqrt{{{(c+c)}^2}+{{(\frac{3c}{2})}^2}}=\frac{5c}{2}$,所以$|PQ|=|FP|-|FQ|=\frac{5c}{2}-\frac{3c}{2}=c$.由已知,线段PQ的长即为PM与QN这两条平行直线间的距离,故直线PM和QN都垂直于直线FP.
因为QN⊥FP,所以$|QN|=|FQ|•tan∠QFN=\frac{3c}{2}×\frac{3}{4}=\frac{9c}{8}$,所以?÷FQN的面积为$\frac{1}{2}|FQ||QN|=\frac{{27{c^2}}}{32}$,同理?÷FPM的面积等于$\frac{{75{c^2}}}{32}$,由四边形PQNM的面积为3c,得$\frac{{75{c^2}}}{32}-\frac{{27{c^2}}}{32}=3c$,整理得c2=2c,又由c>0,得c=2.
所以,椭圆的方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$.
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
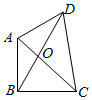 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )| A. | I1<I2<I3 | B. | I1<I3<I2 | C. | I3<I1<I2 | D. | I2<I1<I3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -1或$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | -1或$-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公路段在某一时刻内监测到的车速频率分布直方图如图所示.
某公路段在某一时刻内监测到的车速频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com