
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $-\frac{24}{25}$ | D. | $-\frac{24}{7}$ |
分析 由题意得到tan(x+$\frac{π}{4}$)=$-\frac{1}{7}$,展开后求得tanx,代入万能公式得答案.
解答 解:由tan(x+$\frac{π}{4}$)=$-\frac{1}{7}$,得$\frac{tanx+1}{1-tanx}=-\frac{1}{7}$,解得tanx=$-\frac{4}{3}$.
∴$f(-\frac{1}{7})$=sin2x=$\frac{2tanx}{1+ta{n}^{2}x}=\frac{2×(-\frac{4}{3})}{1+(-\frac{4}{3})^{2}}=\frac{-\frac{8}{3}}{\frac{25}{9}}=-\frac{24}{25}$.
故选:C.
点评 本题考查三角函数的化简求值,考查了万能公式的应用,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{5π}{3}$个单位 | B. | 向左平行移动$\frac{5π}{6}$个单位 | ||
| C. | 向右平行移动$\frac{5π}{3}$个单位 | D. | 向右平行移动$\frac{5π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (-2,-1) | C. | (4,-2) | D. | (-1,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
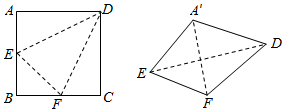 如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为$\frac{\sqrt{6}}{2}$.
如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-2,2) | C. | (-1,2) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com