
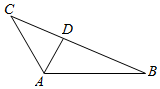
 如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于$\frac{15\sqrt{3}}{4}$,D为边长BC上一点.
如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于$\frac{15\sqrt{3}}{4}$,D为边长BC上一点.分析 (1)由条件利用余弦定理、三角形的面积公式先求得AB的值,可得BC的值.
(2)利用正弦定理求得sin∠ADC 的值,可得cos∠ADC 的值,再利用两角和的余弦公式,求得cos∠CAD=-cos(C+∠ADC)的值.
解答 解:(1)在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于$\frac{1}{2}$•AC•AB•sin∠BAC=$\frac{1}{2}$•3•AB•$\frac{\sqrt{3}}{2}$=$\frac{15\sqrt{3}}{4}$,
∴AB=5,再由余弦定理可得BC2=AB2+AC2-2AB•AC•cos∠BAC=25+9-2×5×3×(-$\frac{1}{2}$)=49,
∴BC=7.
(2)由题意可得cosC=$\frac{{CA}^{2}{+CB}^{2}{-AB}^{2}}{2CA•CB}$=$\frac{11}{14}$,sinC=$\frac{5\sqrt{3}}{14}$.
D为边长BC上一点,当AD=$\frac{15}{8}$时,△ACD中,利用正弦定理可得$\frac{AD}{sinC}$=$\frac{AC}{sin∠ADC}$,即 $\frac{\frac{15}{8}}{\frac{5\sqrt{3}}{14}}$=$\frac{3}{sin∠ADC}$,
求得sin∠ADC=$\frac{4\sqrt{3}}{7}$,∴cos∠ADC=±$\sqrt{{1-sin}^{2}∠ADC}$=±$\frac{1}{7}$.
当 cos∠ADC=$\frac{1}{7}$,cos∠CAD=-cos(C+∠ADC)=-cosC•cos∠ADC+sinC•sin∠ADC
=-$\frac{11}{14}$•$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$•$\frac{4\sqrt{3}}{7}$=$\frac{1}{2}$.
当 cos∠ADC=-$\frac{1}{7}$,cos∠CAD=-cos(C+∠ADC)=-cosC•cos∠ADC+sinC•sin∠ADC
=-$\frac{11}{14}$•(-$\frac{1}{7}$)+$\frac{5\sqrt{3}}{14}$•$\frac{4\sqrt{3}}{7}$=$\frac{71}{98}$.
点评 本题主要考查正弦定理、余弦定理的应用、三角形的面积公式,两角和差的三角函数,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | $(\frac{2}{3},+∞)$ | C. | $(-∞,0)∪(\frac{2}{3},+∞)$ | D. | $(0,\frac{2}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}-1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 喜欢数学课 | 不喜欢数学课 | 合计 | |
| 男生 | 60 | 20 | 80 |
| 女生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
| A. | 4.762 | B. | 9.524 | C. | 0.0119 | D. | 0.0238 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sinα | B. | cosα | C. | -tanα | D. | -$\frac{cosα}{sinα}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y+1=0 | B. | x-y+1=0 | C. | y=2 | D. | y=2-2ln2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com