
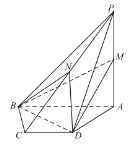
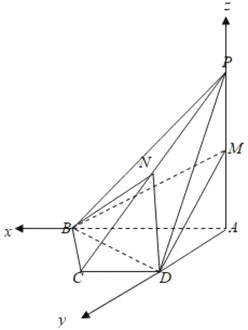
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是一个直角梯形,其中
是一个直角梯形,其中![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点M和点N分别为
,点M和点N分别为![]() 和
和![]() 的中点.
的中点.
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的正弦值;
的正弦值;
(4)求点P到平面![]() 的距离;
的距离;
(5)设点N在平面![]() 内的射影为点H,求线段
内的射影为点H,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]()
【解析】
(1)以![]() 为原点,建立空间直角坐标系,利用向量法,证明
为原点,建立空间直角坐标系,利用向量法,证明![]() 与平面
与平面![]() 的法向量垂直,从而证明直线
的法向量垂直,从而证明直线![]() 平面
平面![]() .
.
(2)求出平面![]() 的法向量,利用向量法,求出直线
的法向量,利用向量法,求出直线![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
(3)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量法,求出二面角
的法向量,利用向量法,求出二面角![]() 的正弦值.
的正弦值.
(4)求出![]() 的坐标,再求出平面
的坐标,再求出平面![]() 的法向量
的法向量![]() ,利用向量法,求出点
,利用向量法,求出点![]() 到平面
到平面![]() 的距离;
的距离;
(5)设点![]() 在平面
在平面![]() 内的射影为点
内的射影为点![]() ,从而表示出
,从而表示出![]() 的坐标,求出
的坐标,求出![]() 到平面
到平面![]() 的距离
的距离![]() ,列出方程组,求出
,列出方程组,求出![]() 点坐标,从而求出
点坐标,从而求出![]() 的长度.
的长度.
(1)四棱锥![]() ,底面
,底面![]() 是一个直角梯形,
是一个直角梯形,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
所以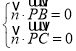 ,
,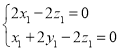 ,
,
取![]() ,则
,则![]() ,
,
所以![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
(2)![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量
的法向量![]() ,
,
则 ,即
,即 ,
,
取![]() ,则
,则![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则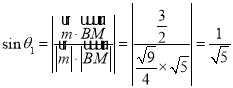 ,
,
所以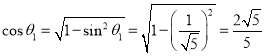 ,
,
所以直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)设平面![]() 的法向量为
的法向量为![]() ,
,
则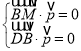 ,即
,即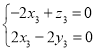 ,
,
取![]() ,得
,得![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则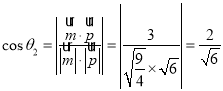 ,
,
所以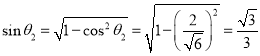 ,
,
所以二面角![]() 的正弦值为
的正弦值为![]() .
.
(4)![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为
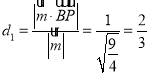 .
.
(5)设点![]() 在平面
在平面![]() 的射影为点
的射影为点![]() ,
,
则![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为 ,
,
根据 ,得
,得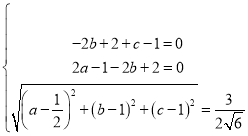
解得![]() ,
,![]() ,
,![]() ,或者
,或者![]() ,
,![]() ,
,![]() (舍)
(舍)
所以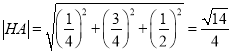 .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,直角梯形
,直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使得平面
为轴旋转得到,且使得平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 满足
满足![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() .
.
(![]() )当点
)当点![]() 是线段
是线段![]() 中点时,求直线
中点时,求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+x-6y+m=0与直线l:x+2y-3=0.
(1)若直线l与圆C没有公共点,求m的取值范围;
(2)若直线l与圆C相交于P、Q两点,O为原点,且OP⊥OQ,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某新上市的电子产品举行为期一个星期(7天)的促销活动,规定购买该电子产品可免费赠送礼品一份,随着促销活动的有效开展,第五天工作人员对前五天中参加活动的人数进行统计,![]() 表示第
表示第![]() 天参加该活动的人数,得到统计表格如下:
天参加该活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测该星期最后一天参加该活动的人数(按四舍五入取到整数).
参考公式: ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com