
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求实数k的值;
(2)判断函数f(x)在(3,+∞)上的单调性,并利用定义证明;
(3)解关于x的不等式f(2x+6)>f(4x+3×2x+3).
【答案】(1)0;(2)详见解析;(3)(-∞,0).
【解析】
(1)根据f(x)是奇函数即可得出![]() ,从而可求出k=0;
,从而可求出k=0;
(2)先写出![]() ,根据单调性定义,设x1>x2>3,然后作差,通分,提取公因式,可判断出f(x1)>f(x2),从而得出f(x)在(3,+∞)上单调递增;
,根据单调性定义,设x1>x2>3,然后作差,通分,提取公因式,可判断出f(x1)>f(x2),从而得出f(x)在(3,+∞)上单调递增;
(3)根据上面得出的f(x)在(3,+∞)上是增函数,可由f(2x+6)>f(4x+3×2x+3)得出2x+6>4x+3×2x+3,解该不等式即可.
解:(1)f(x)是奇函数;
∴f(-x)=-f(x);
∴![]() ;
;
∴x2-kx+9=x2+kx+9;
∴-kx=kx;
∴k=0;
(2)![]() 在(3,+∞)上是增函数,证明如下:
在(3,+∞)上是增函数,证明如下:
设x1>x2>3,则:![]() =
=![]() ;
;
∵x1>x2>3;
∴x1-x2>0,x1x2>9,![]() ;
;
∴![]() ;
;
∴f(x1)-f(x2)>0;
∴f(x1)>f(x2);
∴f(x)在(3,+∞)上是增函数;
(3)由(2)知,f(x)在(3,+∞)上是增函数,且2x+6>3,4x+3×2x+3>3;
∴由f(2x+6)>f(4x+3×2x+3)得,2x+6>4x+3×2x+3;
∴(2x)2+2×2x-3<0;
∴-3<2x<1;
∴x<0;
∴原不等式的解集为(-∞,0).


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10. 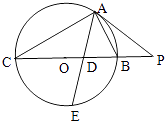
(1)求证:AC=2AB;
(2)求ADDE的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: ![]() (t为参数,α≠0)经过椭圆C:
(t为参数,α≠0)经过椭圆C: ![]() (φ为参数)的左焦点F.
(φ为参数)的左焦点F.
(1)求实数m的值;
(2)设直线l与椭圆C交于A、B两点,求|FA|×|FB|取最小值时,直线l的倾斜角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学的![]() 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车,每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车,每车限坐![]() 名同学(乘同一辆车的
名同学(乘同一辆车的![]() 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的![]() 名同学中恰有
名同学中恰有![]() 名同学是来自于同一年级的乘坐方式共有( ).
名同学是来自于同一年级的乘坐方式共有( ).
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在篮球比赛中,如果某位球员的得分,篮板,助攻,抢断,盖帽中有两个值达到![]() 或
或![]() 以上,就称该球员拿到了两双.下表是某球员在最近五场比赛中的数据统计:
以上,就称该球员拿到了两双.下表是某球员在最近五场比赛中的数据统计:
场次 | 得分 | 篮板 | 助攻 | 抢断 | 盖帽 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )从上述比赛中任选
)从上述比赛中任选![]() 场,求该球员拿到“两双”的概率.
场,求该球员拿到“两双”的概率.
(![]() )从上述比赛中任选
)从上述比赛中任选![]() 场,设该球员拿到“两双”的次数为
场,设该球员拿到“两双”的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(![]() )假设各场比赛互相独立,将该球员在上述比赛中获得“两双”的频率作为概率,设其在接下来的三场比赛中获得“两双”的次数为
)假设各场比赛互相独立,将该球员在上述比赛中获得“两双”的频率作为概率,设其在接下来的三场比赛中获得“两双”的次数为![]() ,试比赛
,试比赛![]() 与
与![]() 的大小关系(只需写出结论).
的大小关系(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱柱![]() 的正(主)视图和侧(左)视图如图所示,设
的正(主)视图和侧(左)视图如图所示,设![]() ,
,![]() 的中心分别为
的中心分别为![]() ,
, ![]() ,现将此三棱柱绕直线
,现将此三棱柱绕直线![]() 旋转,射线
旋转,射线![]() 旋转所成角为
旋转所成角为![]() 弧度(
弧度(![]() 可以取到任意一个实数),对应的俯视图的面积为
可以取到任意一个实数),对应的俯视图的面积为![]() ,则函数
,则函数![]() 的最大值为__________,最小正周期为__________.
的最大值为__________,最小正周期为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|).
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com