
| A. | f(sin$\frac{1}{2}$)<f(cos$\frac{1}{2}$) | B. | f(sin$\frac{π}{3}$)>f(cos$\frac{π}{3}$) | C. | f(sin1)<f(cos1) | D. | f(cos$\frac{3}{2}$)<f(sin$\frac{3}{2}$) |
分析 确定偶函数f(x)在(-1,0)上是增函数,f(x)在(0,1)上是减函数,即可得出结论.
解答 解:x∈[3,4]时,f(x)=2x,故偶函数f(x)在[3,4]上是增函数,
又定义在R上的偶函数f(x)满足f(x)=f(x+2),故函数的周期是2
所以偶函数f(x)在(-1,0)上是增函数,
所以f(x)在(0,1)上是减函数,
对于A,sin$\frac{1}{2}$<cos$\frac{1}{2}$,∴f(sin$\frac{1}{2}$)>f(cos$\frac{1}{2}$),
对于B,sin$\frac{π}{3}$>cos$\frac{π}{3}$,∴f(sin$\frac{π}{3}$)<f(cos$\frac{π}{3}$);
对于C,sin1>cos1,∴,f(sin1)<f(cos1);
对于D,-cos$\frac{3}{2}$>sin$\frac{3}{2}$,∴f(-cos$\frac{3}{2}$)>f(sin$\frac{3}{2}$),∴f(cos$\frac{3}{2}$)>f(sin$\frac{3}{2}$),
故选:C.
点评 本题考查函数的周期性与函数的单调性比较大小,构思新颖,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:解答题
| ?x+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{5π}{12}$ | $\frac{11π}{12}$ | |||
| Asin(?x+φ) | 0 | 3 | 0 | -3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
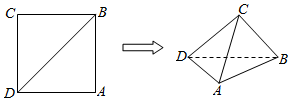
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{12}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a,+∞) | |
| B. | (-∞,a) | |
| C. | 当a>1时,解集是(a,+∞);当0<a<1时,解集是(-∞,a) | |
| D. | 当a>1时,解集是(-∞,a);当0<a<1时,解集是(a,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com