

| A、1﹕3 | B、1﹕4 |
| C、1﹕5 | D、1﹕6 |
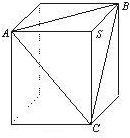 解:设长方体的长、宽、高分别为a,b,c,
解:设长方体的长、宽、高分别为a,b,c,| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |


科目:高中数学 来源: 题型:
 如图,曲线y=sinx在圆x2+y2=π2内的部分与x轴围成的阴影部分区域记为Ω,随机向圆内投掷一个点A,则点A落在区域Ω的概率为( )
如图,曲线y=sinx在圆x2+y2=π2内的部分与x轴围成的阴影部分区域记为Ω,随机向圆内投掷一个点A,则点A落在区域Ω的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
| A、9 | B、12 |
| C、18 | D、以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 | ||||
| B、由a1=1,an=3n-1(n≥2),求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 | ||||
C、由圆x2+y2=r2(r>0)的面积S=πr2,猜想出椭圆
| ||||
| D、利用等差数列的性质推理得到等比数列的相关性质 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 2014 |
| A、1008 | B、2013 |
| C、2014 | D、2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| A、(-∞,3) | ||||
| B、(3,+∞) | ||||
C、(-∞,
| ||||
D、(-∞,-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com