
分析 根据双曲线的离心率,求出a的值,结合双曲线的定义进行转化求解即可.
解答 解:∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{2}=1$的离心率等于$\frac{{\sqrt{6}}}{2}$,
∴e2=$\frac{{c}^{2}}{{a}^{2}}$=$\frac{{a}^{2}+2}{{a}^{2}}=\frac{3}{2}$,∴a=2,c=$\sqrt{6}$.
设|PF1|=m,|PF2|=n,
则|m-n|=2a=4,
则由余弦定理可得24=m2+n2-mn,∴24=(m-n)2+mn=16+mn,
即mn=8.
则(m+n)2=(m-n)2+4mn=4a2+4mn=16+4×8=48,
则m+n=$\sqrt{48}$=4$\sqrt{3}$,
故答案为:4$\sqrt{3}$.
点评 本题考查双曲线的方程与性质,根据双曲线的离心率求出a的值,结合双曲线的定义进行转化是解决本题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:填空题
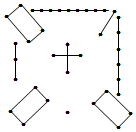 洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.
洛书古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上有如图所示图案,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,洛书中蕴含的规律奥妙无穷,比如:42+92+22=82+12+62.据此你能得到类似等式是42+32+82=22+72+62.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否喜欢数学 | 是 | 否 | 合计 |
| 男生 | 30 | 10 | 40 |
| 女生 | 20 | 20 | 40 |
| 合计 | 50 | 30 | 80 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0[来源:] | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果a∥α,b∥α,那么a∥b | |
| B. | 如果a∥b,a∥α,b?α,那么b∥α | |
| C. | 如果a∥b,那么α平行于经过b的任何平面 | |
| D. | 如果a∥α,那么a与α内的任何直线平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
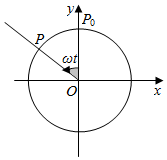 如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).
如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com