
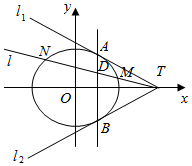
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.分析 (1)联立$\left\{\begin{array}{l}{y=±\frac{1}{2}(x-4)}\\{3{x}^{2}+{a}^{2}{y}^{2}-3{a}^{2}=0}\end{array}\right.$,得(3+$\frac{{a}^{2}}{4}$)x2-2a2x+a2=0,直线与椭圆相切,利用的判别式能求出a.
(2)T(4,0),设直线l的方程为x=my+4,联立$\left\{\begin{array}{l}{x=my+4}\\{3{x}^{2}+4{y}^{2}-12=0}\end{array}\right.$,消去x,得(3m2+4)y2+24my+4m2+36=0,由此利用韦达定理、相似形性质,结合已知条件能证明$\frac{|TD|}{|TM|}$+$\frac{|TD|}{|TN|}$为定值.
解答 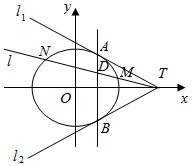 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4)
解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4)
∴联立$\left\{\begin{array}{l}{y=±\frac{1}{2}(x-4)}\\{3{x}^{2}+{a}^{2}{y}^{2}-3{a}^{2}=0}\end{array}\right.$,消去y并化简,得(3+$\frac{{a}^{2}}{4}$)x2-2a2x+a2=0,
∵直线与椭圆相切,
∴△=4a4-4(3+$\frac{{a}^{2}}{4}$)a2=3a4-12a2=0,
由a>0,解得a=2.
证明:(2)由(1)得T(4,0),
不妨设直线l的方程为x=my+4,由题意得m≠0,设M(x1,y1),N(x2,y2),
联立$\left\{\begin{array}{l}{x=my+4}\\{3{x}^{2}+4{y}^{2}-12=0}\end{array}\right.$,消去x,得(3m2+4)y2+24my+4m2+36=0,
由根与系数的关系,得${y}_{1}+{y}_{2}=-\frac{24m}{3{m}^{2}+4}$,${y}_{1}{y}_{2}=\frac{36}{3{m}^{2}+4}$,
又切点的横坐标应满足方程(3+$\frac{{a}^{2}}{4}$)x2-2a2x+a2=0,即4x2-8x+4=0,
即xA=xB=1,∴直线AB的方程为x=1.
当直线l与x轴重合时,|TD|=3,|TM|=2,|TN|=6,
∴$\frac{|TD|}{|TM|}$+$\frac{|TD|}{|TN|}$=$\frac{3}{2}+\frac{3}{6}=2$为定值;
当直线l与x轴不重合时,m≠0,则点D(1,-$\frac{3}{m}$),
根据相似形,得$\frac{|TD|}{|TM|}$=$\frac{|{y}_{0}-{y}_{T}|}{|{y}_{M}-{y}_{T}|}$=$\frac{|{y}_{D}|}{|{y}_{1}|}$,$\frac{|TD|}{|TN|}$=$\frac{|{y}_{D}-{y}_{T}|}{|{y}_{N}-{y}_{T}|}$=$\frac{|{y}_{D}|}{|{y}_{2}|}$,
∴$\frac{|TD|}{|TM|}$+$\frac{|TD|}{|TN|}$=$\frac{|{y}_{D}|}{|{y}_{1}|}+\frac{|{y}_{D}|}{|{y}_{2}|}$=$\frac{|{y}_{D}|•|{y}_{1}+{y}_{2}|}{|{y}_{1}{y}_{2}|}$(y1,y2同号)
=$\frac{|-\frac{3}{m}|•|-\frac{24m}{3{m}^{2}+4}|}{|\frac{36}{3{m}^{2}+4}|}$=2为定值.
∴$\frac{|TD|}{|TM|}$+$\frac{|TD|}{|TN|}$为定值2.
点评 本题考查实数值的求法,考查代数式和为定值的证明,是中档题,解题时要认真审题,注意椭圆性质、直线与椭圆相切、韦达定理的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N⊆M | B. | M⊆N | C. | M∩N=∅ | D. | M∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{\sqrt{2}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| t | 30 | 40 | p | 50 | 70 |
| m | 2 | 4 | 5 | 6 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}-\overrightarrow{b}$ | B. | $\overrightarrow{a}+\overrightarrow{b}$ | C. | $\overrightarrow{b}-\overrightarrow{a}$ | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com