
分析 (1)利用数学语言准确叙述出余弦定理的内容.
(2)采用坐标法证明,方法是以A为原点,AB所在的直线为x轴建立平面直角坐标系,表示出点C和点B的坐标,利用两点间的距离公式表示出|BC|的平方,化简后即可得到a2=b2+c2-2bccosA,同理可证b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
解答 解:(1)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦之积的两倍;或在△ABC中,a,b,c为A,B,C的对边,有a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.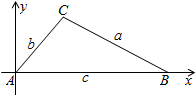
(2)证明:已知△ABC中A,B,C所对边分别为a,b,c,
以A为原点,AB所在直线为x轴建立直角坐标系,
则C(bcosA,bsinA),B(c,0),
∴a2=|BC|2=(bcosA-c)2+(bsinA)2
=b2cos2A-2bccosA+c2+b2sin2A
=b2+c2-2bccosA,
同理可证b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
点评 此题考查余弦定理及其证明,以及对命题形式出现的证明题,要写出已知求证再进行证明,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | -$\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{{(-1)}^n}+1}}{2}$ | B. | $cos\frac{nπ}{2}$ | C. | $cos\frac{(n+1)π}{2}$ | D. | $cos\frac{(n+2)π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 20世纪30年代,德国数学家洛萨---科拉茨提出猜想:任给一个正整数x,如果x是偶数,就将它减半;如果x是奇数,则将它乘3加1,不断重复这样的运算,经过有限步后,一定可以得到1,这就是著名的“3x+1”猜想.如图是验证“3x+1”猜想的一个程序框图,若输出n的值为8,则输入正整数m的所有可能值的个数为( )
20世纪30年代,德国数学家洛萨---科拉茨提出猜想:任给一个正整数x,如果x是偶数,就将它减半;如果x是奇数,则将它乘3加1,不断重复这样的运算,经过有限步后,一定可以得到1,这就是著名的“3x+1”猜想.如图是验证“3x+1”猜想的一个程序框图,若输出n的值为8,则输入正整数m的所有可能值的个数为( )| A. | 3 | B. | 4 | C. | 6 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com