
分析 (1)将a=1代入f(x),解不等式即可;
(2)问题转化为 $\frac{1}{x}+x>-a$在[2,3]恒成立,令$g(x)=x+\frac{1}{x}$,根据函数的单调性求出a的范围即可;
(3)问题转化为(x-1)[(a-4)x-1]=0,通过讨论a的范围,结合方程解的个数,确定a的范围即可.
解答 解:(1)当a=1时,$f(x)={2^{\frac{1}{x}+1}}$,
由f(x)>4得${2^{\frac{1}{x}+1}}>4={2^2}$,…..(1分)
所以 $\frac{1}{x}+1>2⇒\frac{1}{x}>1⇒0<x<1$,
即不等式的解集是(0,1).…(3分)
(2)因为f(x)>2-x在[2,3]恒成立,
即${2^{\frac{1}{x}+a}}>{2^{-x}}$在[2,3]恒成立,
即$\frac{1}{x}+a>-x$在[2,3]恒成立,
即 $\frac{1}{x}+x>-a$在[2,3]恒成立…..(5分)
令$g(x)=x+\frac{1}{x}$,由${g^'}(x)=1-\frac{1}{x^2}>0$在[2,3]恒成立,
所以g(x)在区间[2,3]单调递增,…(7分)
所以g(x)的最小值为$g(2)=\frac{5}{2}$,
所以$-a<\frac{5}{2}$,即$a>-\frac{5}{2}$…..….…(9分)
(3)由题意得${2^{\frac{1}{x}+a}}-{2^{(a-4)x+2a-5}}=0$
所以$\frac{1}{x}+a=(a-4)x+2a-5$,
即(a-4)x2+(2a-5)x-1=0,
即(x-1)[(a-4)x-1]=0….(11分)
①当a=4时,x=-1∈(-2,0),满足题意;….(12分)
②当a≠4时,
i.$x=\frac{1}{a-4}=-1$,即a=3,满足题意;…(13分)
ii.$x=\frac{1}{a-4}≤-2$或$x=\frac{1}{a-4}≥0$解$\frac{7}{2}≤a<4$或a>4..(15分)
从而 $a∈\{3\}∪[\frac{7}{2},+∞)$…(16分)
点评 本题考查了解不等式问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | |r|越大,相关程度越小 | B. | |r|越小,相关程度越大 | ||
| C. | |r|趋近于0时,没有非线性相关关系 | D. | |r|越接近于1时,线性相关程度越强 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | B. | $-\frac{2}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AD}$ | C. | $\frac{2}{3}\overrightarrow{AB}-\overrightarrow{AD}$ | D. | $-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d>$\frac{8}{3}$ | B. | d<3 | C. | $\frac{8}{3}$≤d<3 | D. | $\frac{4}{3}$<d≤$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
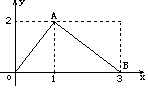 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com