练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．设集合P={x|x=$\frac{k}{3}$+$\frac{1}{6}$，k∈Z}，Q={x|x=$\frac{k}{6}$+$\frac{1}{3}$，k∈Z}，则（　　）
    A．P=QB．P?QC．P?QD．P∩Q=∅

    分析 P={x|x=$\frac{2k+1}{6}$，k∈Z}，Q={x|x=$\frac{k+2}{6}$，k∈Z}．由于k+2既可以为偶数，也可以为奇数，即可得出关系．

    解答 解：P={x|x=$\frac{k}{3}$+$\frac{1}{6}$，k∈Z}={x|x=$\frac{2k+1}{6}$，k∈Z}．
    Q={x|x=$\frac{k}{6}$+$\frac{1}{3}$，k∈Z}，Q={x|x=$\frac{k+2}{6}$，k∈Z}．
    由于k+2既可以为偶数，也可以为奇数，
    ∴P?Q，
    故选：B．

    点评 本题考查了集合的运算性质、元素与集合之间的关系，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知复数z=$\frac{{{i^{2016}}}}{1-i}$，则复数$\overline z$在复平面上对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

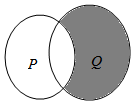    5．已知集合P={x|y=$\frac{1}{\sqrt{4-x}}$}，Q={y|y=log2（x2+4）}，集合P与集合Q所对应的韦恩图如图所示，则图中阴影部分表示的集合是（　　）
    A．{x|2≤x＜4}B．{x|x＜2}C．{x|x≥4}D．{x|x＜2，或x≥4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知集合A={a1，a2，a3，a4，a5，a6，a7}，A∪B={a1，a2，a3，a4，a5，a6，a7，…，a100}，则所有满足题意的集合B的个数为128．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．作下列函数的简图：
    （1）y=$\frac{1}{2}$（cosx+|cosx|）；
    （2）y=sin|x-$\frac{π}{2}$|

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知关于x的一元二次方程x2+ax+1=0，分别求满足下列条件下的实数a的取值范围．
    （1）两根均大于-1；
    （2）一个根大于-1，另一个根小于-1；
    （3）两个根均在（-1，2）内．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知sin（α+β）•cosβ-cos（α+β）•sinβ=$\frac{3}{5}$，则cos2α=$\frac{7}{25}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．对于函数f（x），如果存在锐角θ使得f（x）的图象绕坐标原点逆时针旋转角θ，所得曲线仍是一函数，则称函数f（x）具备角θ的旋转性，下列函数具有角$\frac{π}{4}$的旋转性的是（　　）
    A．$y=\sqrt{{x^2}-1}$B．y=x2C．y=2xD．y=lnx

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若函数f（x）=x2+bx+c，满足f（-1）=f（5），则f（1），f（2），f（4）的大小关系为f（4）＞f（1）＞f（2）．

    查看答案和解析>>

    同步练习册答案