
分析 △ABF面积等于△AOF和△BOF的面积之和,△AOF和△BOF的面积相等,A到x轴的距离h应最大,又h的最大值为b,从而得到△ABF面积的最大值;设出Q的坐标,利用对称知识,集合椭圆方程推出椭圆几何量之间的关系,然后求解离心率即可.
解答 解:△ABF面积等于△AOF和△BOF的面积之和,
设A到x轴的距离为h,由AB为过椭圆中心的弦,
则B到x轴的距离也为h,
可得△AOF和△BOF的面积相等,
故△ABF面积等于$\frac{1}{2}$c•2h=ch,又h的最大值为b,
则有△ABF面积的最大值是bc;
设Q(m,n),由题意可得$\left\{\begin{array}{l}{\frac{n}{m-c}=-\frac{c}{b}}\\{\frac{1}{2}n=\frac{b}{c}•\frac{m+c}{2}}\end{array}\right.$,
可得:m=$\frac{{c}^{3}-c{b}^{2}}{{a}^{2}}$,n=$\frac{2b{c}^{2}}{{a}^{2}}$,
代入椭圆方程可得:$\frac{(\frac{{c}^{3}-c{b}^{2}}{{a}^{2}})^{2}}{{a}^{2}}$+$\frac{(\frac{2b{c}^{2}}{{a}^{2}})^{2}}{{b}^{2}}$=1,
解得e2(4e4-4e2+1)+4e2=1,
可得4e6+e2-1=0.
即4e6-2e4+2e4-e2+2e2-1=0,
可得(2e2-1)(2e4+e2+1)=0
解得e=$\frac{\sqrt{2}}{2}$.
故答案为:bc,$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的方程和简单性质的应用,用分割法求△ABF的面积,利用△AOF和△BOF是同底等高的两个三角形和运用对称知识是解题的关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,
四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E为PA的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
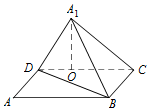 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1在平面BCD上的射影O恰在CD上,即A1O⊥平面DBC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.
已知在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接三角形△AEF的三条边都相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com