
| A. | 1:2 | B. | 1:3 | C. | 1:1 | D. | 1:4 |
分析 如图所示,由$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=2$\overrightarrow{AB}$,可得$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=2$(\overrightarrow{AM}+\overrightarrow{MB})$,化为:$3\overrightarrow{AM}$=$\overrightarrow{BC}$,因此AM∥BC,3AM=BC,∠CBA=π-∠BAM,再利用三角形面积计算公式即可得出.
解答 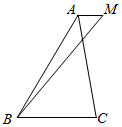 解:如图所示,∵$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=2$\overrightarrow{AB}$
解:如图所示,∵$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=2$\overrightarrow{AB}$
∴$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=2$(\overrightarrow{AM}+\overrightarrow{MB})$,
化为:$3\overrightarrow{AM}$=$\overrightarrow{BC}$,
∴AM∥BC,3AM=BC,∠CBA=π-∠BAM,
∴sin∠CBA=sin∠BAM,
则$\frac{{S}_{△ABM}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}AB•AMsin∠BAM}{\frac{1}{2}BA•BCsin∠ABC}$=$\frac{1}{3}$.
故选:B.
点评 本题考查了向量的三角形法则、向量共线定理、三角形面积计算公式,考查了数形结合方法、推理能力与计算能力,属于中档题.


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
| 频数 | 20 | 10 | 12 | a | b | 50 |
| 频率 | 0.4 | 0.2 | p | 0.12 | q | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2018 | B. | 2017 | C. | 2016 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | (-1,0) | C. | (-2,+∞) | D. | (-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥2 | B. | m≤-2 | C. | m≤-2或m≥2 | D. | -2≤m≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{14}$ | B. | $\frac{9}{28}$ | C. | $\frac{3}{28}$ | D. | $\frac{3}{56}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com