
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 上的动点
上的动点![]() 到两焦点的距离之和为4,当点
到两焦点的距离之和为4,当点![]() 运动到椭圆
运动到椭圆![]() 的上顶点时,直线
的上顶点时,直线![]() 恰与以原点
恰与以原点![]() 为圆心,以椭圆
为圆心,以椭圆![]() 的离心率为半径的圆相切.
的离心率为半径的圆相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,若
,若![]() 交直线
交直线![]() 于
于![]() 两点.问以
两点.问以![]() 为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
为直径的圆是否过定点?若过定点,请求出该定点坐标;若不过定点,请说明理由.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取![]() 名同学(男
名同学(男![]() 人,女
人,女![]() 人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
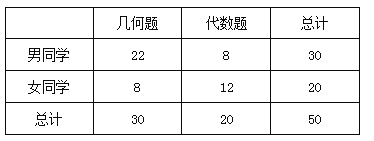
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的![]() 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为
名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为![]() ,求
,求![]() 的分布列和
的分布列和![]() .
.
附表及公式: 

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高中男生中随机选取100名学生,将他们的体重(单位: ![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.

(1)估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);
(2)若要从体重在![]() ,
, ![]() ,
, ![]() 三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在
三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场做促销活动,凡是一家三口一起来商场购物的家庭,均可参加返现活动,活动规则如下:商家在箱中装入20个大小相同的球,其中6个是红球,其余都是黑球;每个家庭只能参加一次活动,参加活动的三口人,每人从中任取一球,只能取一次,且每人取球后均放回;若取到黑球则获得4元返现金,若取到红球则获得12元返现金.若某家庭参与了该活动,则该家庭获得的返现金额的期望是( ).
A. 22.4 B. 21.6 C. 20.8 D. 19.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com