
分析 (Ⅰ)利用绝对值不等式,结合关于x的不等式|x+1|-|x-2|>|a-3|的解集是空集,即可求实数a的取值范围;
(Ⅱ)利用柯西不等式,结合对任意正实数x,y,不等式$\sqrt{2x}$+$\sqrt{3y}$<k$\sqrt{8x+6y}$恒成立,求实数k的取值范围.
解答 解:(Ⅰ)∵||x+1|-|x-2||≤|(x+1)-(x-2)|=3,
∴-3≤|x+1|-|x-2|≤3,
∵关于x的不等式|x+1|-|x-2|>|a-3|的解集是空集
∴|a-3|≥3,
∴a≥6或a≤0;
(Ⅱ)由柯西不等式可得($\frac{1}{4}$+$\frac{1}{2}$)(8x+6y)≥($\sqrt{2x}+\sqrt{3y}$)2,
∴$\frac{\sqrt{2x}+\sqrt{3y}}{\sqrt{8x+6y}}$≤$\frac{\sqrt{3}}{2}$,
∵对任意正实数x,y,不等式$\sqrt{2x}$+$\sqrt{3y}$<k$\sqrt{8x+6y}$恒成立,
∴k>$\frac{\sqrt{3}}{2}$,即实数k的取值范围是($\frac{\sqrt{3}}{2}$,+∞).
点评 本题考查绝对值不等式,考查柯西不等式的运用,考查恒成立问题,正确转化是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标伸长为原来的2倍 | |
| B. | 横坐标伸长为原来的2倍,纵坐标伸长为原来的2倍 | |
| C. | 横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标缩短为原来的$\frac{1}{2}$倍 | |
| D. | 横坐标伸长为原来的2倍,纵坐标缩短为原来的$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
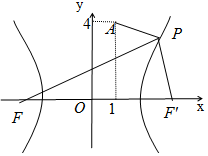 已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:
已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com