
分析 根据函数是一个奇函数先求出f(1),根据函数满足f(x+3)=f(x),得到函数是一个周期函数,利用周期性和奇函数得到要求的结果.
解答 解:∵f(x)是奇函数,∴f(-x)=-f(x)
所以f(1)=-f(-1)=-1
f(2)=f((-1)+3)=f(-1)=1
∵f(0)=f(3)=-f(-3)=-f(-3+3)=-f(0)
所以f(0)=0
而f(10)=f(7)=f(4)=f(1)
f(9)=f(6)=f(3)=f(0)
f(8)=f(5)=f(2)
∴f(1)+f(2)+…+f(10)
=4f(1)+3f(2)+3f(0)
=-4+3=-1
故答案为-1.
点评 本题考查函数的奇偶性和函数的周期性,本题解题的关键是看出在要求的十个变量的函数值中,可以分成三部分,分别求出结果.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
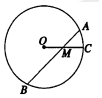 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
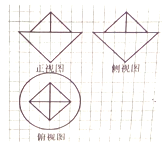 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$ | B. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$-8 | C. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$ | D. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,2] | B. | [-7,-6] | C. | [-9,-4] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | y=1 | C. | y-1=$\sqrt{2}$(x+1) | D. | y-1=2$\sqrt{2}$(x+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
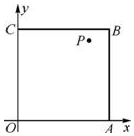 如图,在边长为1的正方形OABC内任取一点P(x,y).
如图,在边长为1的正方形OABC内任取一点P(x,y).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com