
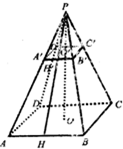
 如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.
如图所示,正四棱锥P-ABCD被过棱锥高上O′点且平行底面的平面A′B′C′D′所截,得到正四棱台OO′和较小的棱锥PO′,其中O′分PO为$\frac{PO′}{OO′}$=$\frac{1}{2}$,侧棱PA长为15cm,小棱锥底面边长A′B′为6cm.分析 (1)计算出棱台的上、下底的边长,高,可得截得棱台的体积;
(2)由等体积计算棱锥P-ABCD的内切球的半径,即可求出棱锥P-ABCD的内切球的表面积.
解答 解:(1)由A′B′∥AB得$\frac{PA′}{PA}=\frac{A′B′}{AB}=\frac{PO′}{PO}$,
∴$\frac{PA′}{15}=\frac{6}{AB}$=$\frac{1}{3}$,
∴PA′=5,AB=18,
∵PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=3$\sqrt{7}$
∴OO′=$\frac{2}{3}$PO=2$\sqrt{7}$,
∴V台=$\frac{1}{3}$(36+182+$\sqrt{36×1{8}^{2}}$)•2$\sqrt{7}$=312$\sqrt{7}$(cm3)…(6分)
(2)作轴截面图如下,设球心为E,半径为R,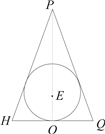
由PH=PQ=12,HQ=AB=18,PO=$\sqrt{1{2}^{2}-{9}^{2}}$=3$\sqrt{7}$,则
∵S△PHQ=$\frac{1}{2}$(PH+PQ+HQ)R,
∴$\frac{1}{2}×18×3\sqrt{7}$=$\frac{1}{2}$(12+12+18)R,
∴R=$\frac{9}{\sqrt{7}}$,
∴棱锥P-ABCD的内切球的表面积为4πR2=$\frac{324}{7}$π(cm2)…(12分)
点评 本题考查棱台的体积,考查棱锥P-ABCD的内切球的表面积,考查学生的计算能力,求出棱锥P-ABCD的内切球的半径是关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-2,3),4 | B. | (-2,3),16 | C. | (2,-3),4 | D. | (4,-6),16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | 优 | 良 | 及格 | 不及格 |
| 优 | 1 | 3 | 1 | 1 |
| 良 | 1 | 0 | 7 | 6 |
| 及格 | 2 | 4 | 0 | 9 |
| 不及格 | 1 | b | 7 | a+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 钝角三角形 | ||
| C. | 锐角三角形 | D. | 以上三种情况都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com